Equivariances & Graphical Neural Networks

Description of this Post

1 Title

Slide 1

2 Organisation

Slide 2

3 Lecture overview

Slide 3

4 Graphs! They’re everywhere

Slide 4

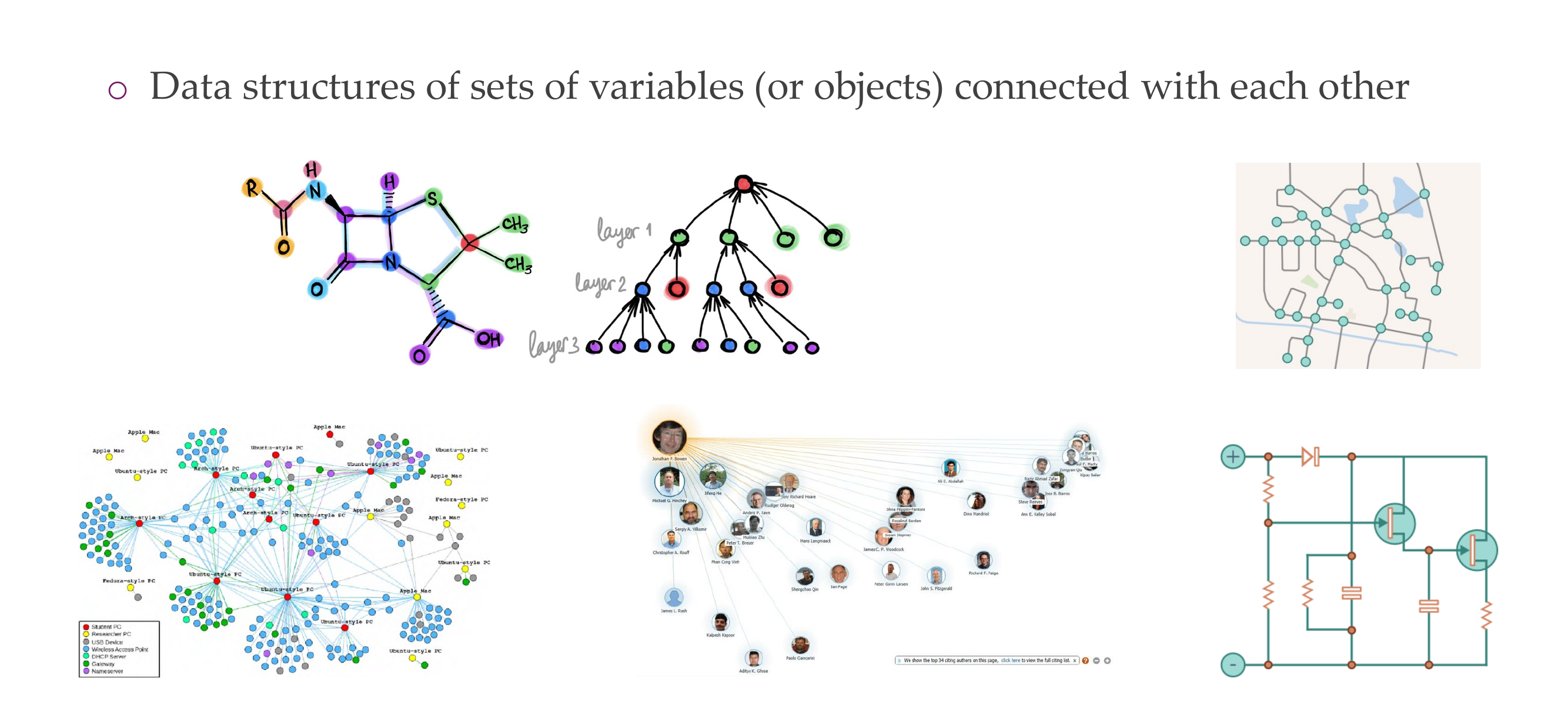
5 What are graphs?

Slide 5

6 What are graphs?

Slide 6

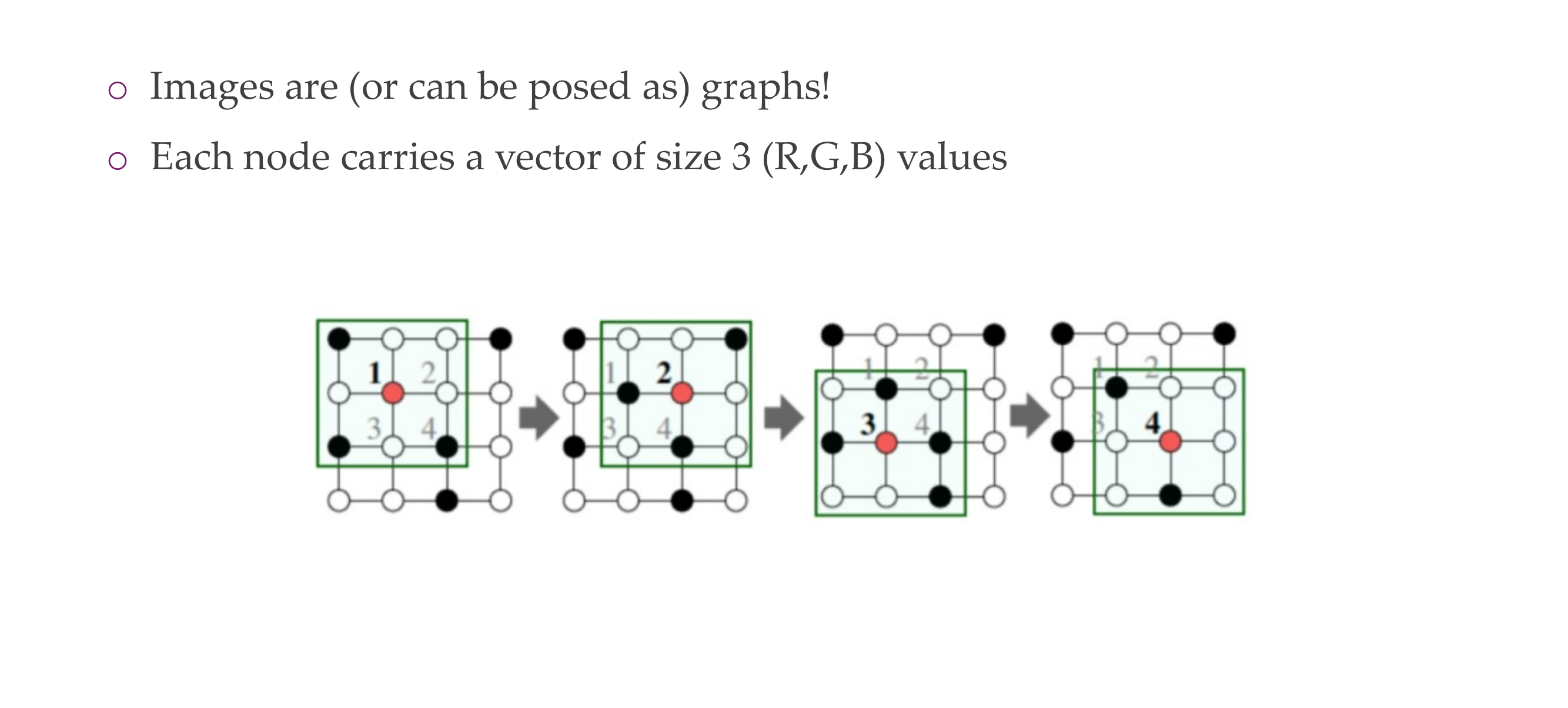
7 Graphs as geometry.

Slide 7

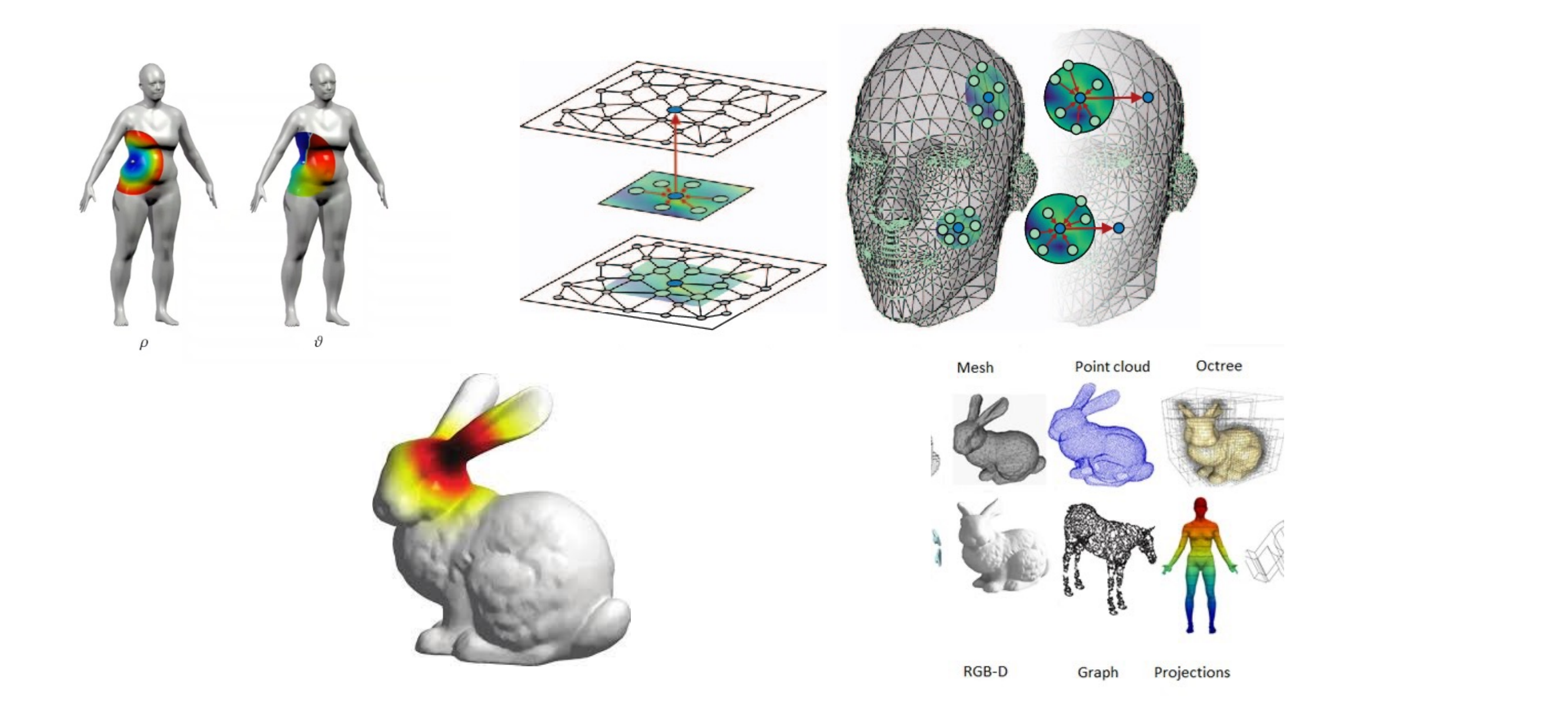
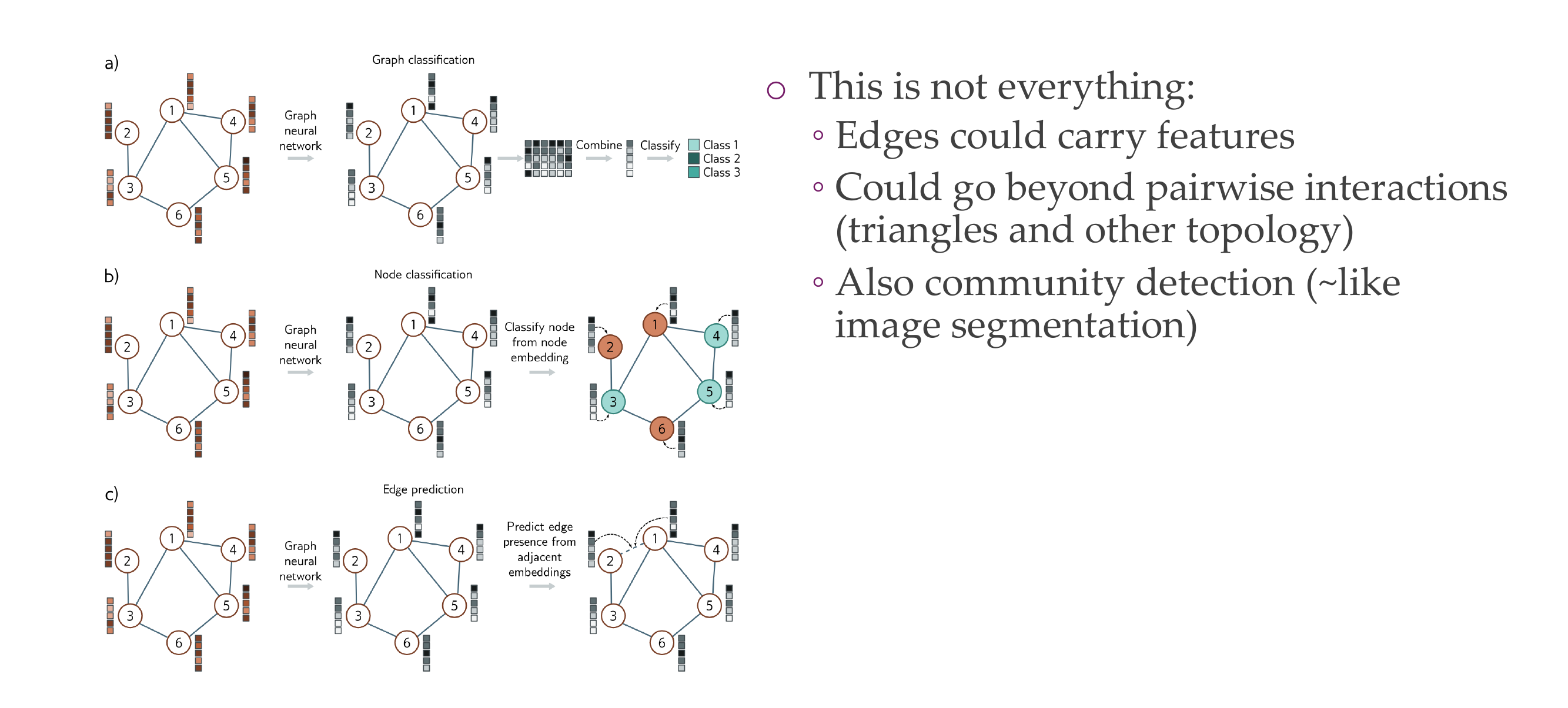
8 1) Classifying graphs

Slide 8

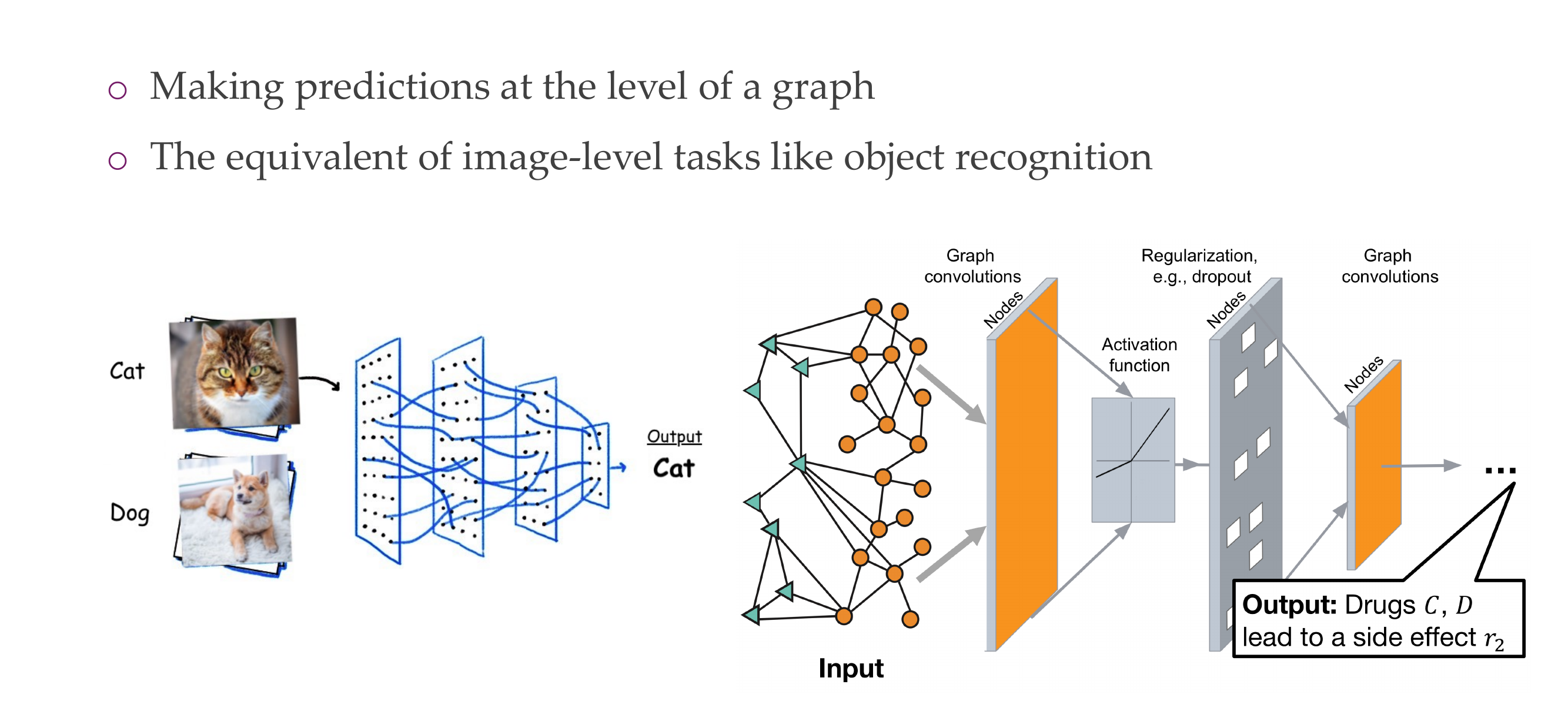
9 2) Classifying nodes

Slide 9

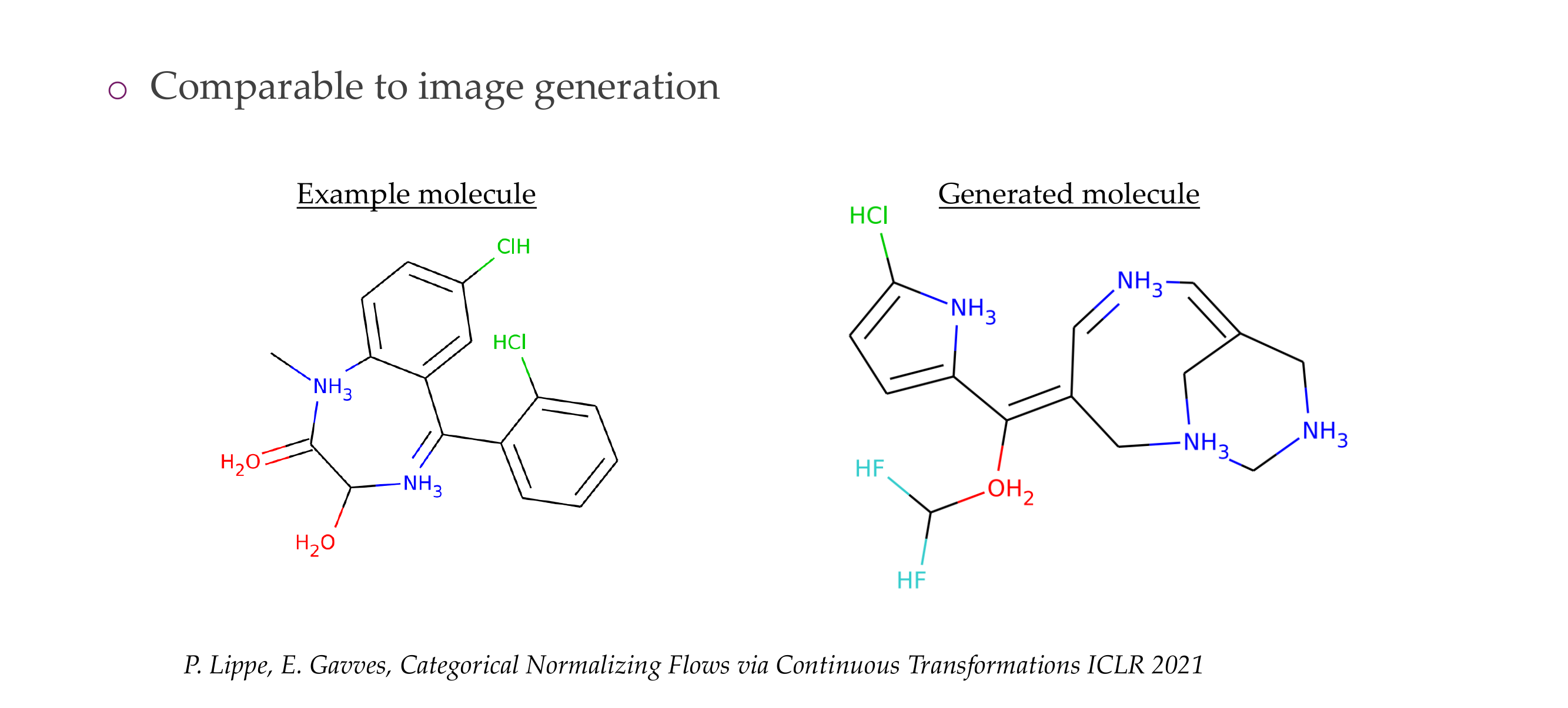
10 3) Graph generation

Slide 10

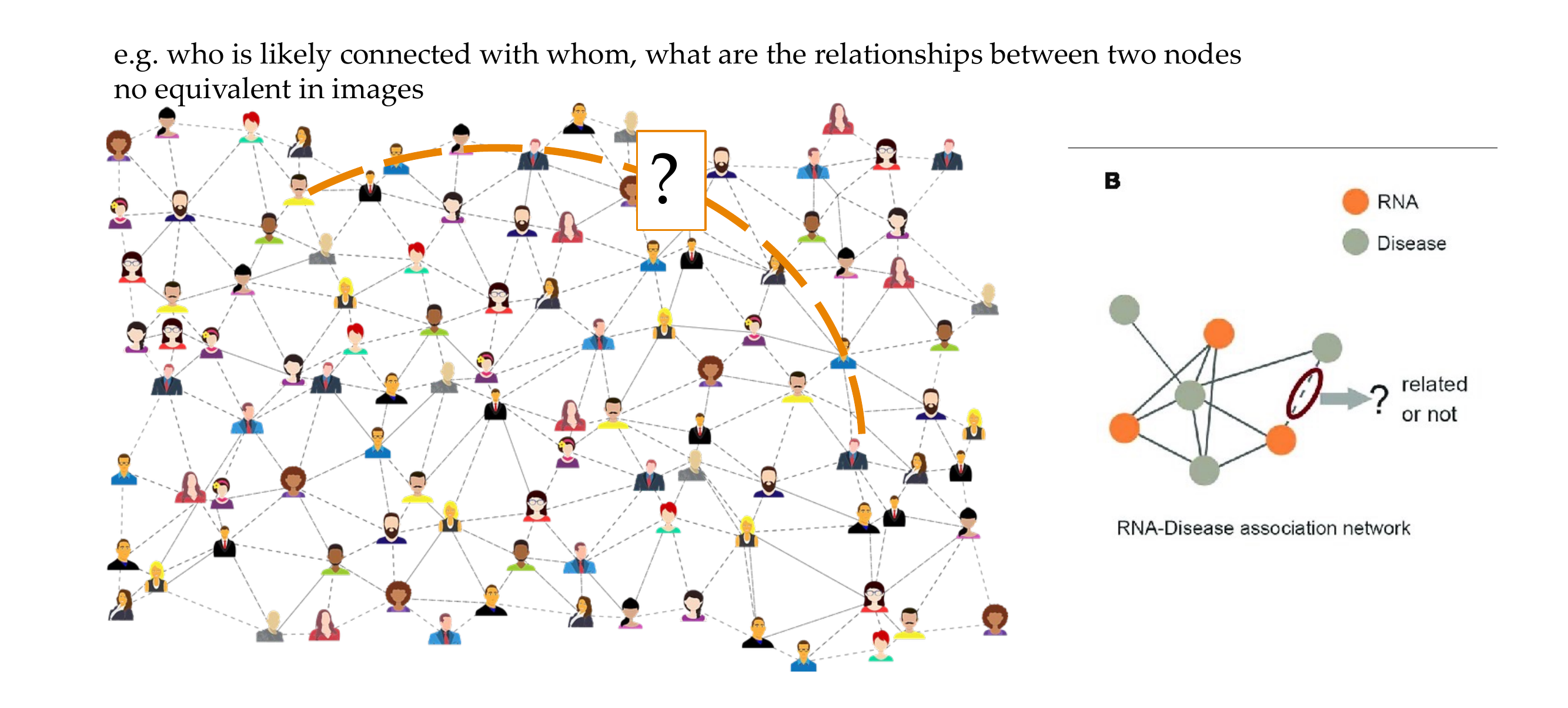
11 4) Link/Edge prediction

Slide 11

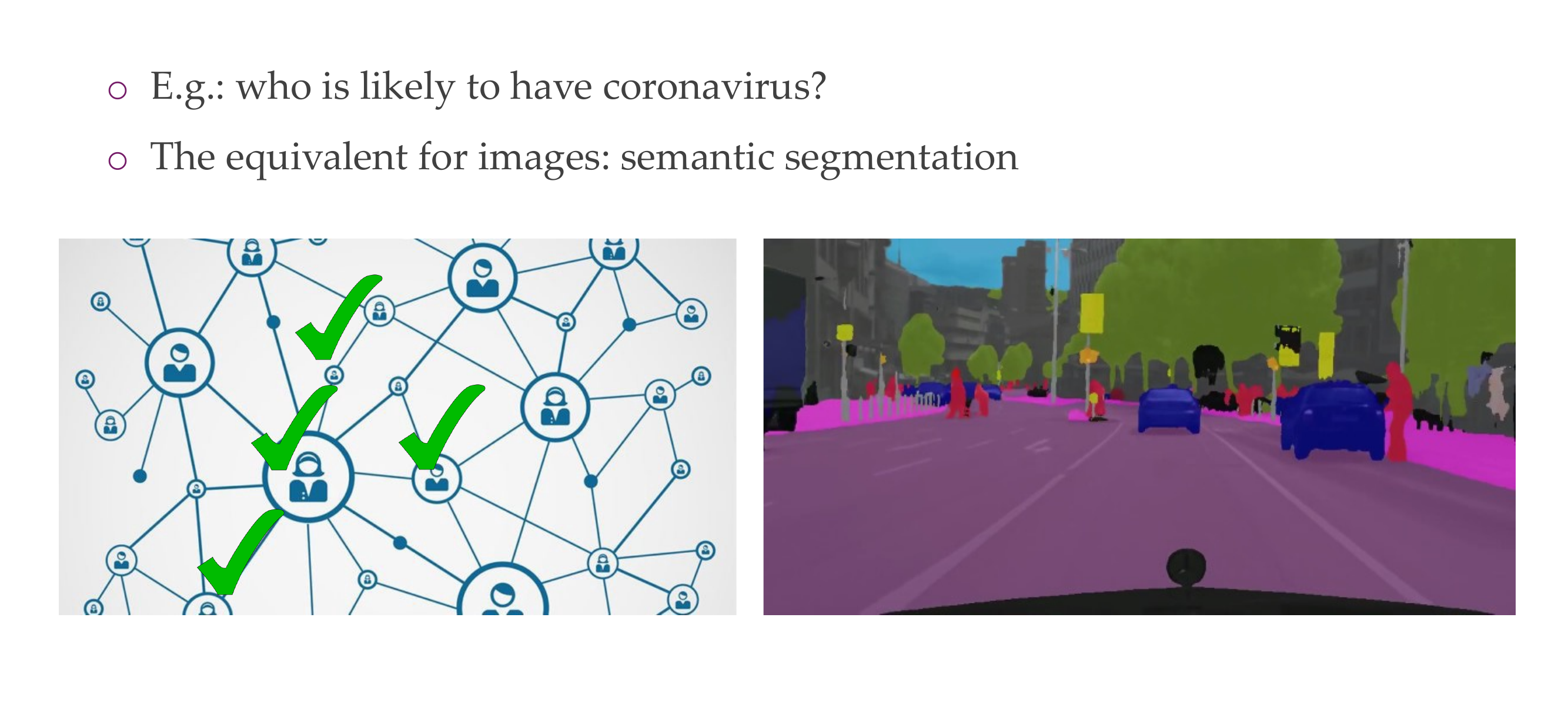
12 Three tasks visualized: here with nodes that carry features

Slide 12

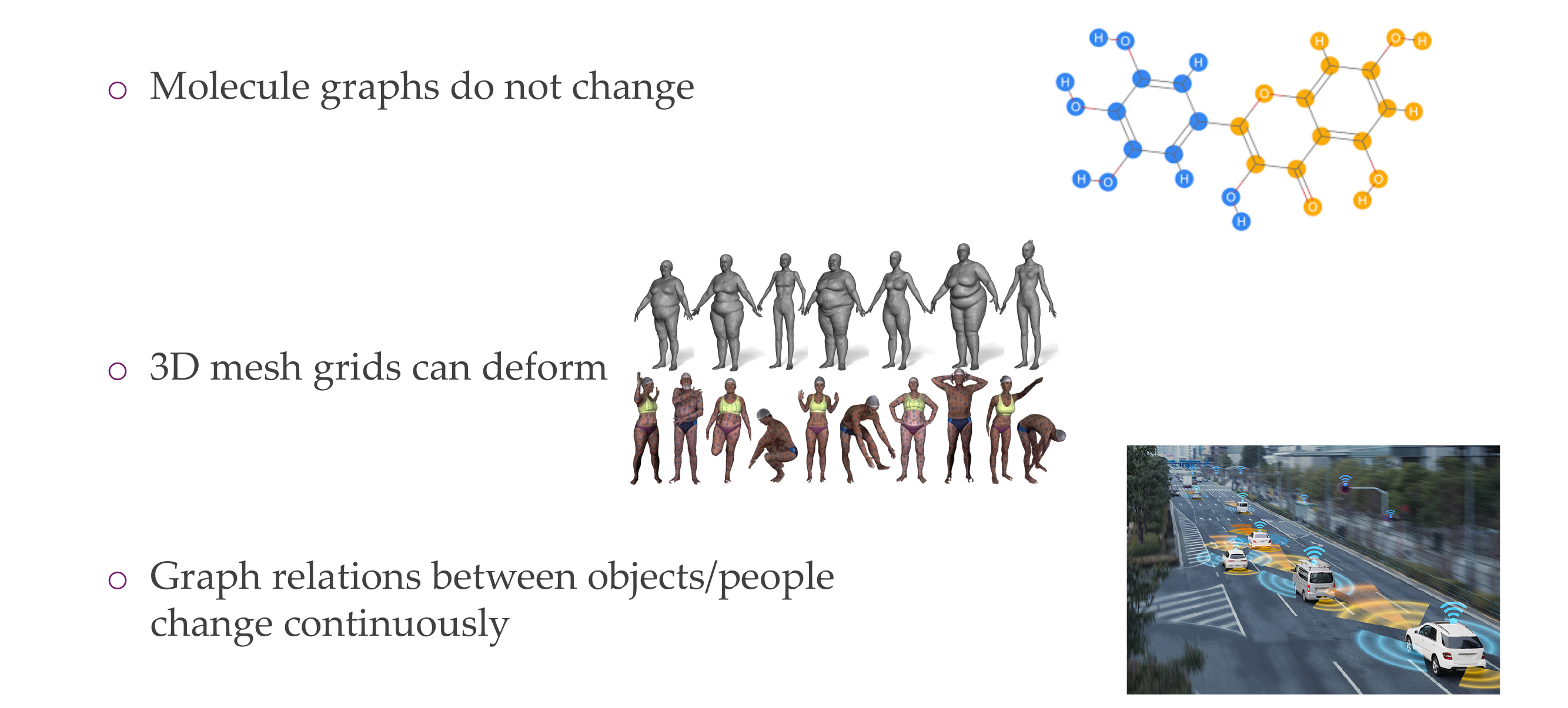
13 Graphs can be static, varying, or even evolving with time

Slide 13

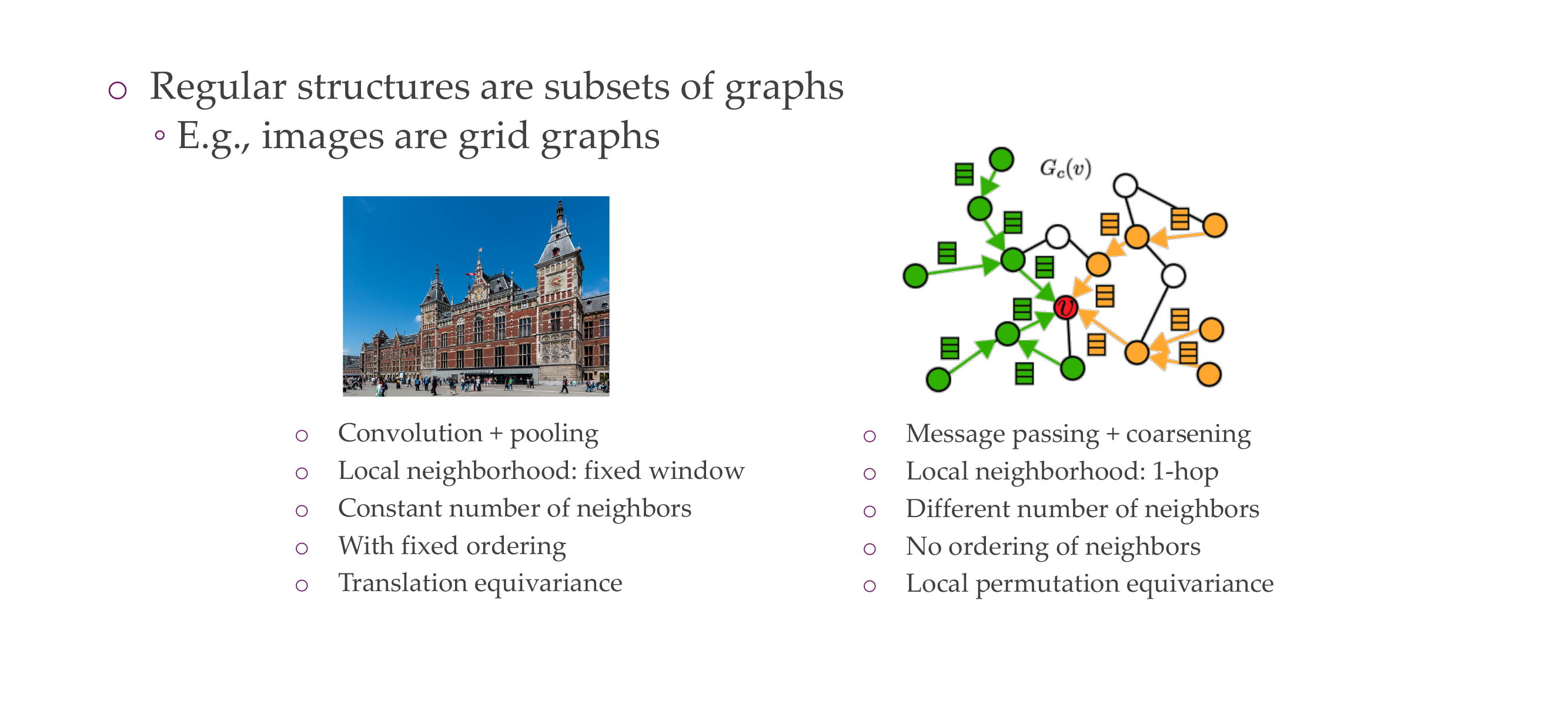
14 Regular structures vs graphs

Slide 14

15 Title

Slide 15

16 Directed graphs

Slide 16

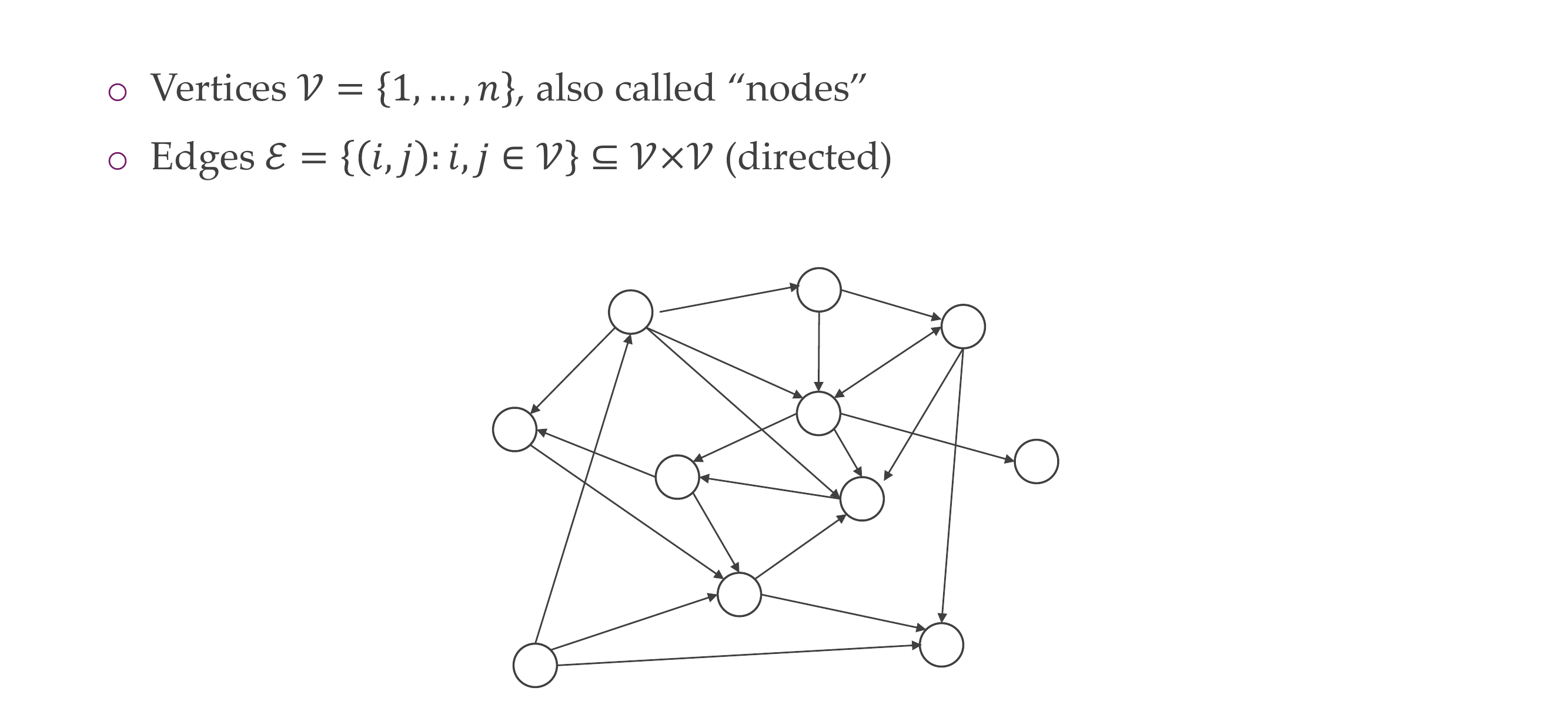
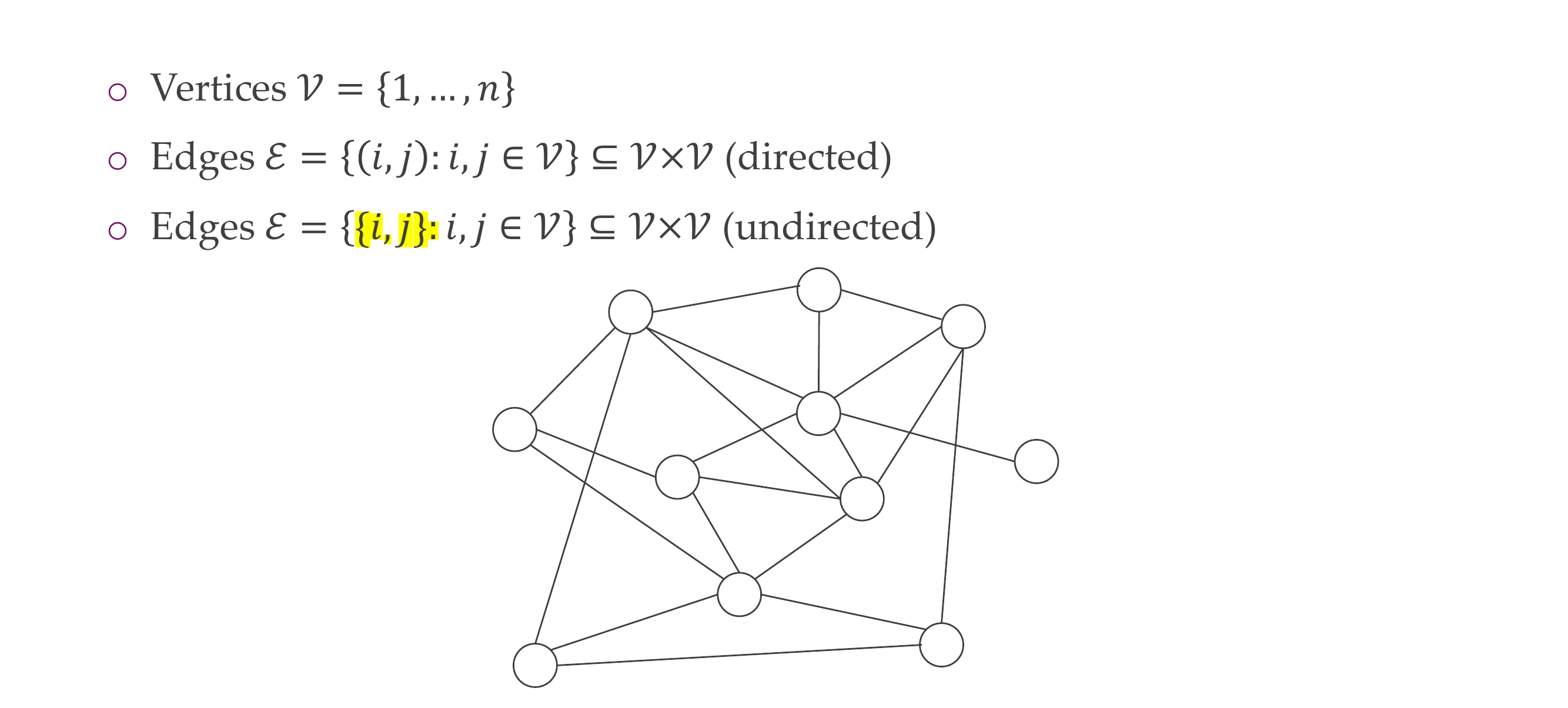
17 Undirected graphs

Slide 17

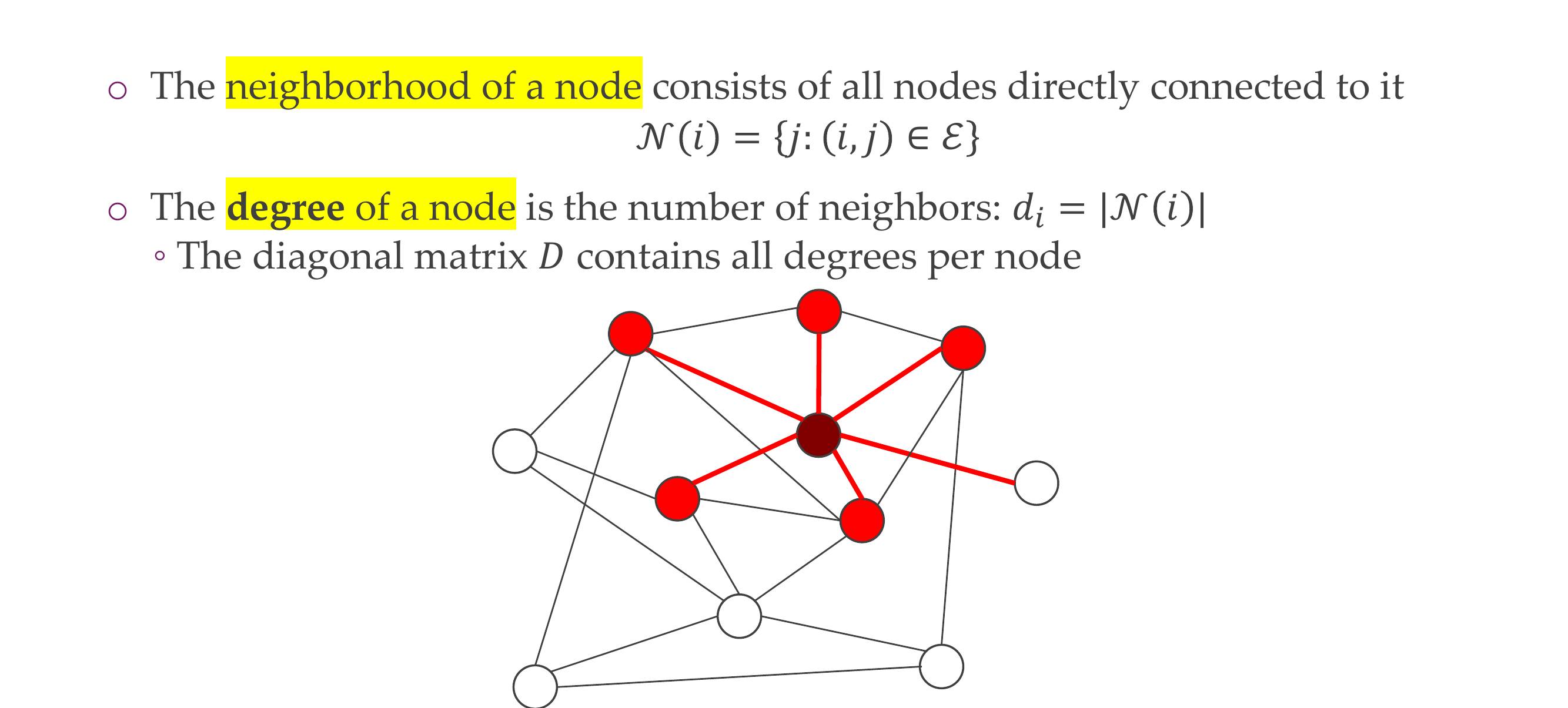
18 Graph neighborhood

Slide 18

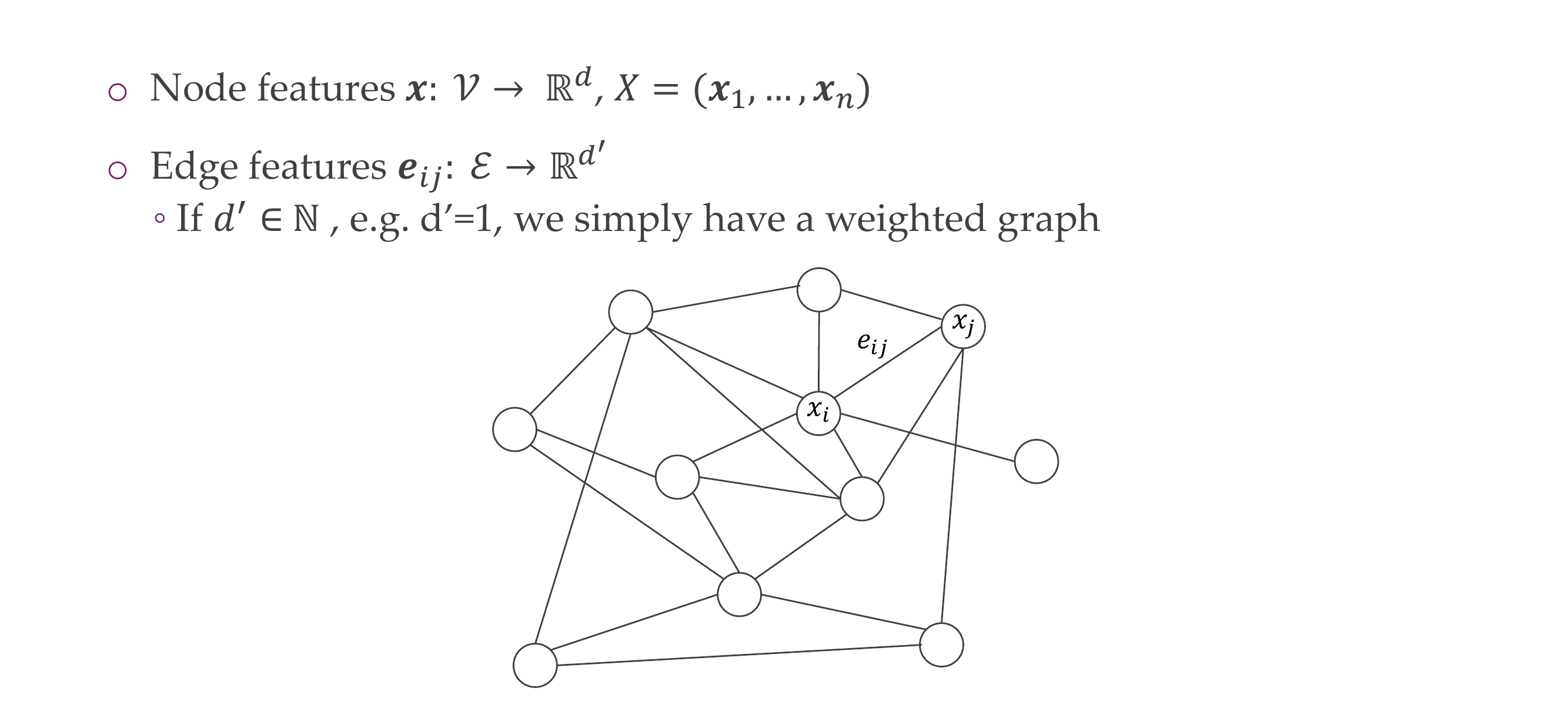
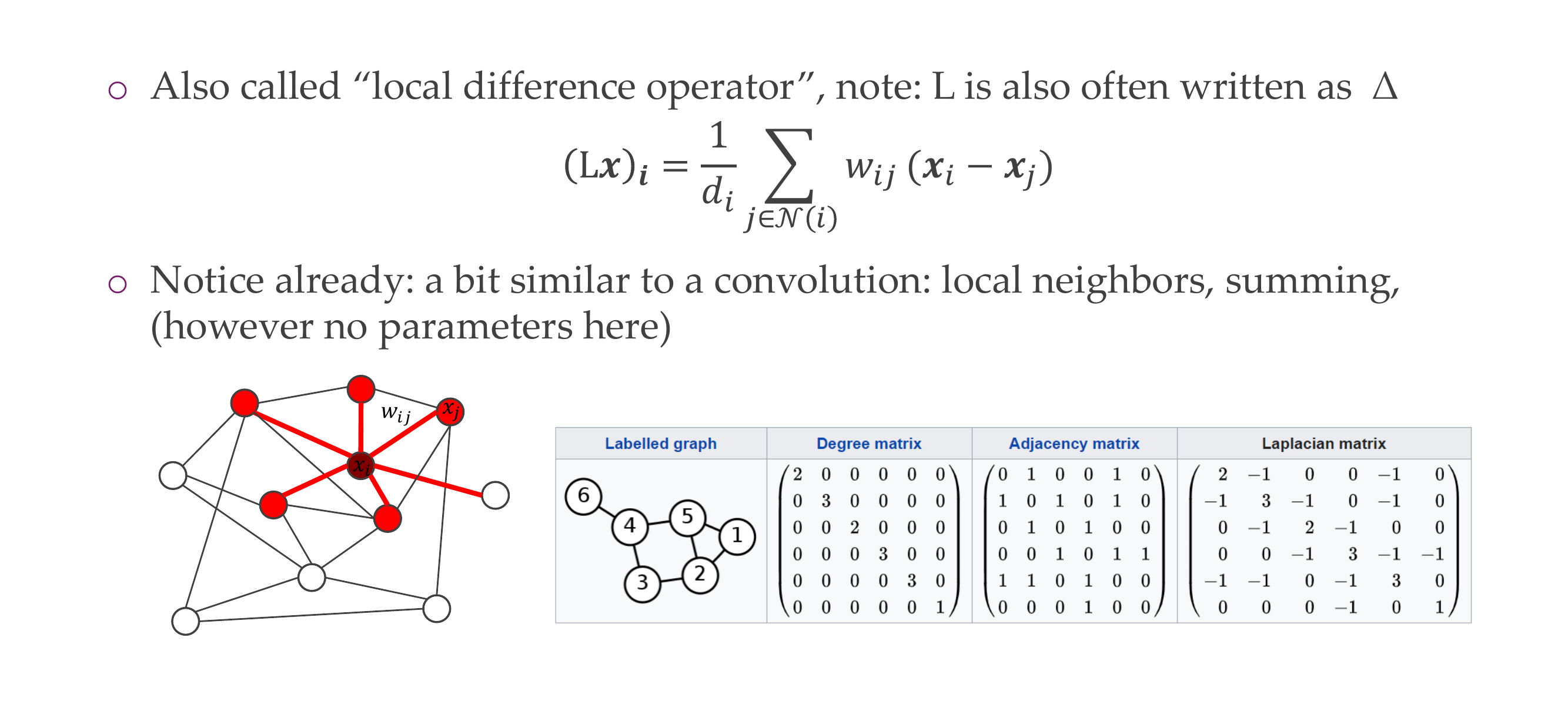
19 Attributes

Slide 19

The attention score is measured by these softmax

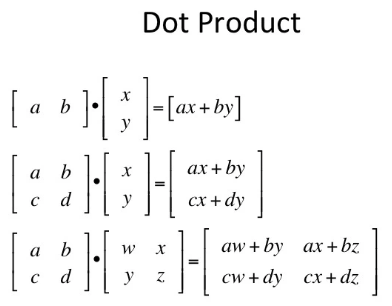
The dot product here it ends up being 2x3 again

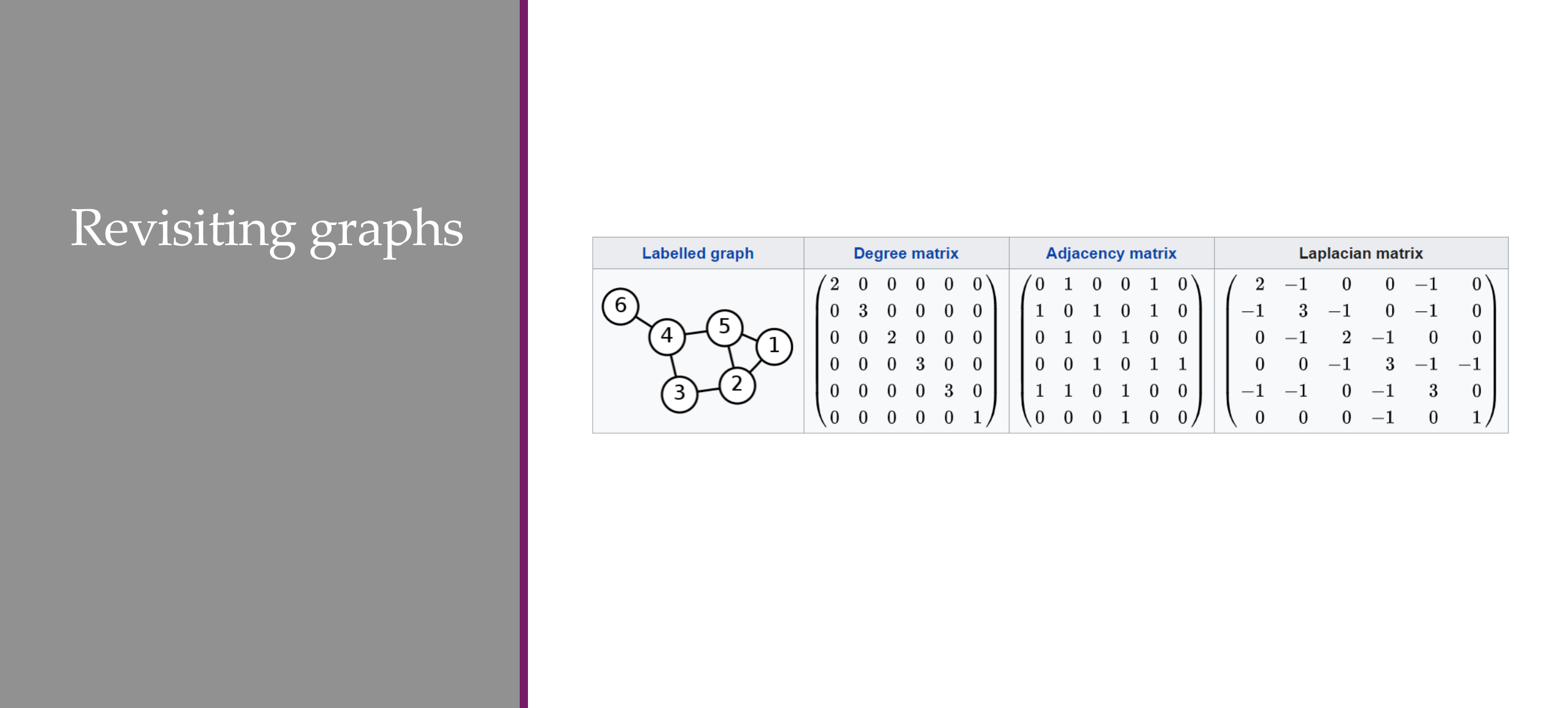
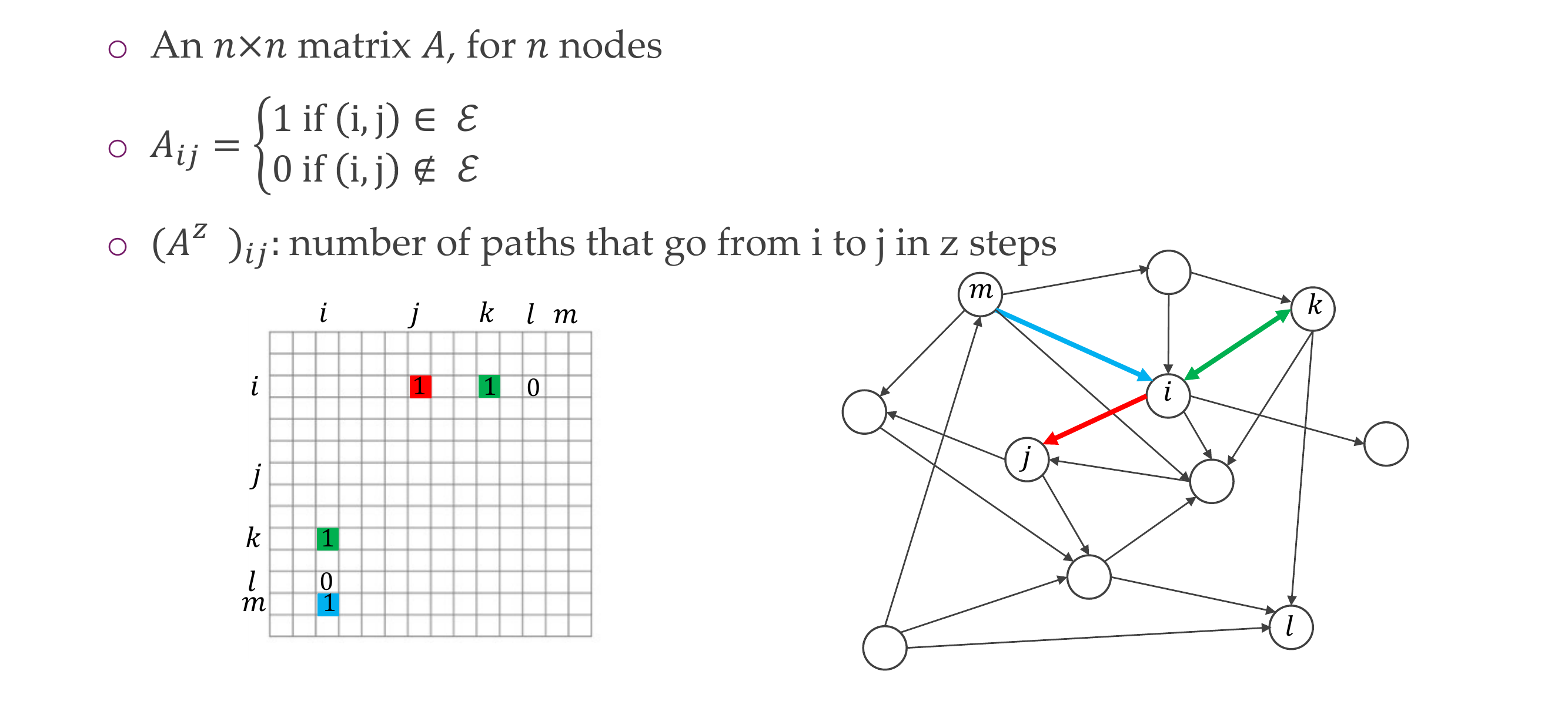
20 Adjacency matrix

Slide 20

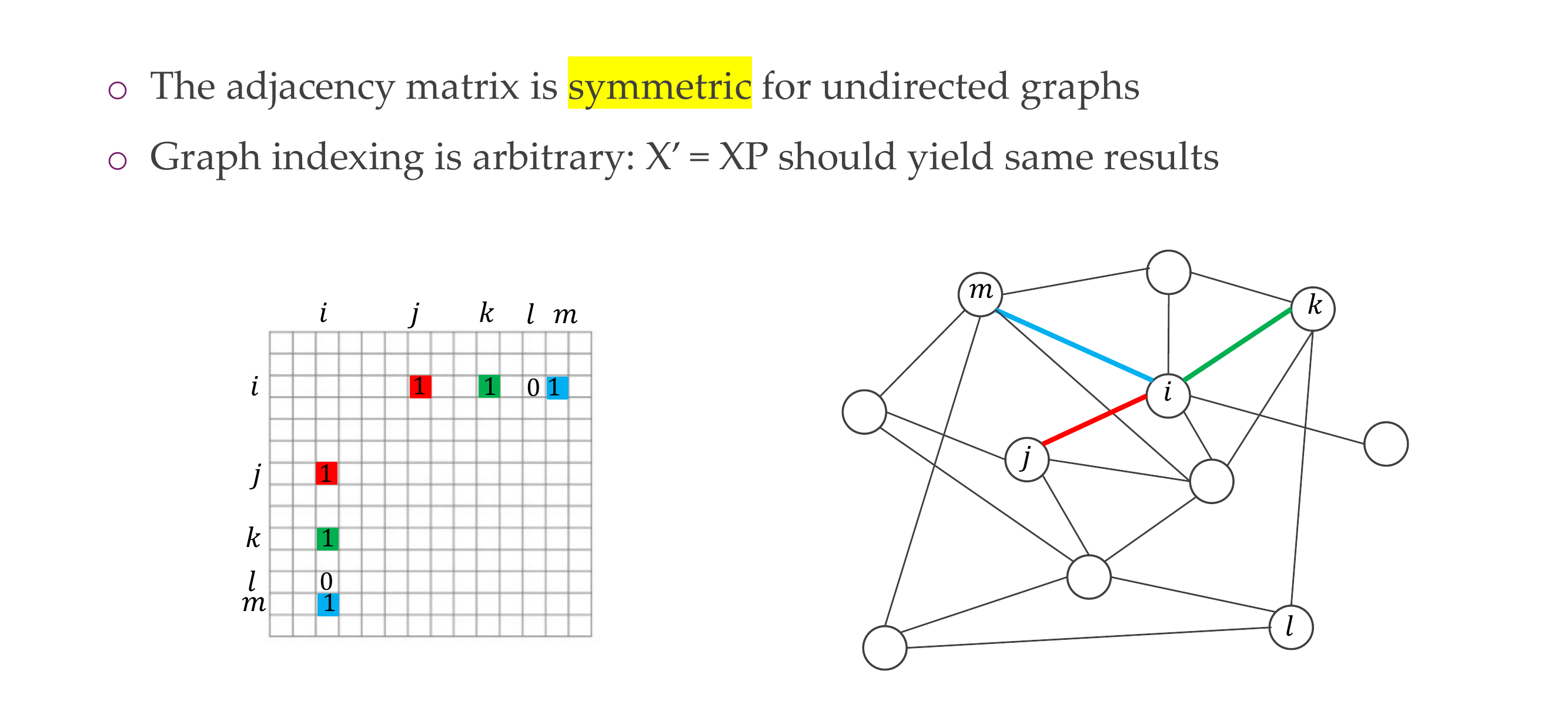
21 Adjacency matrix for undirected graphs

Slide 21

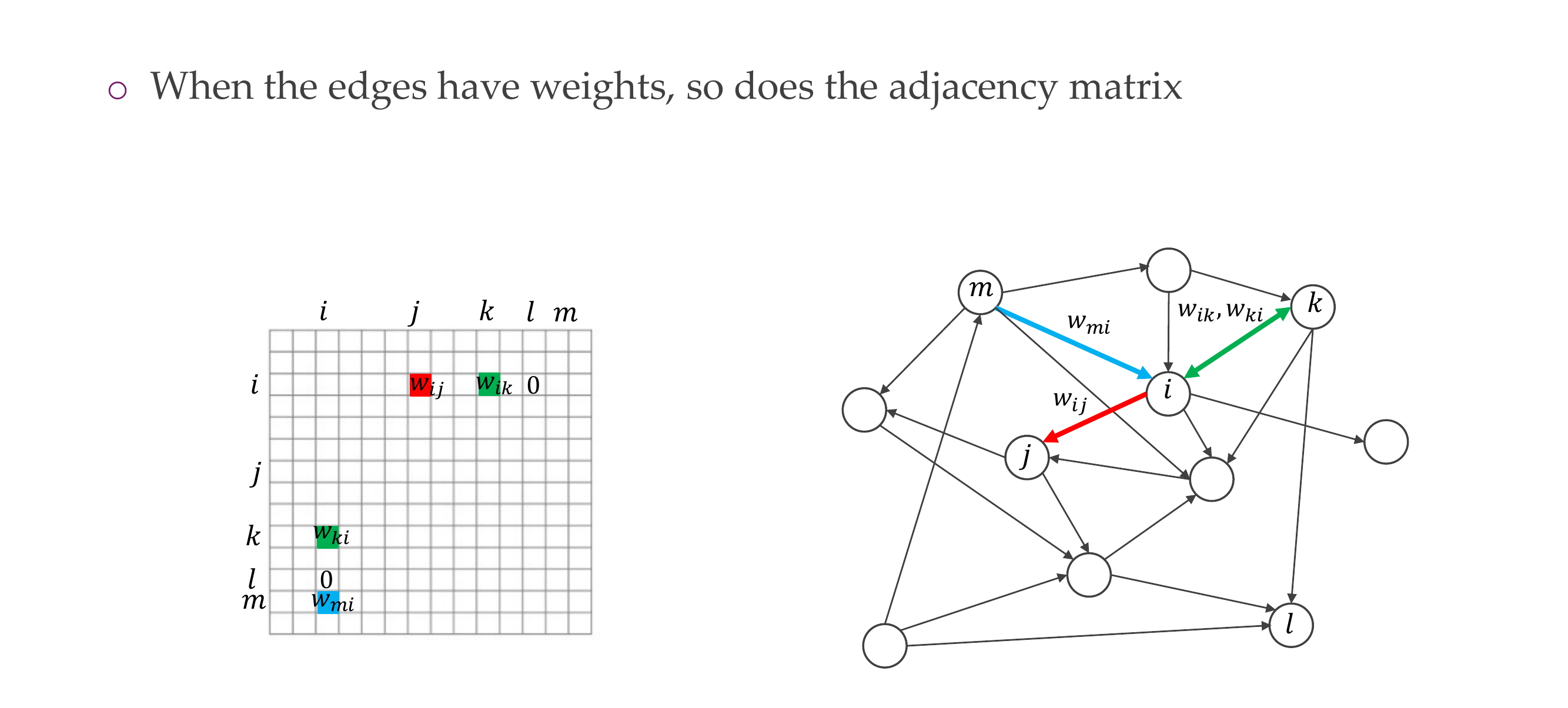
22 Weighted adjacency matrix

Slide 22

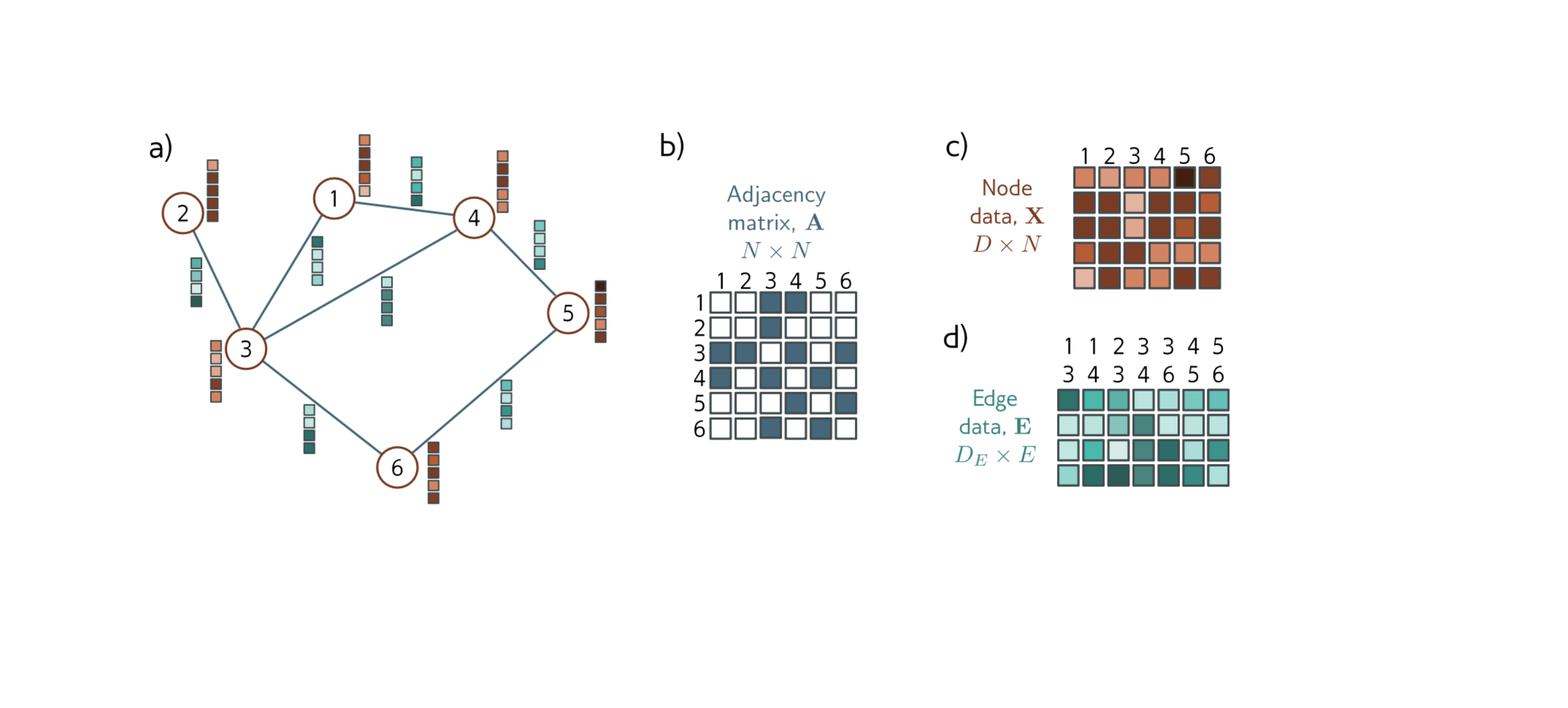
23 Graph representation for us

Slide 23

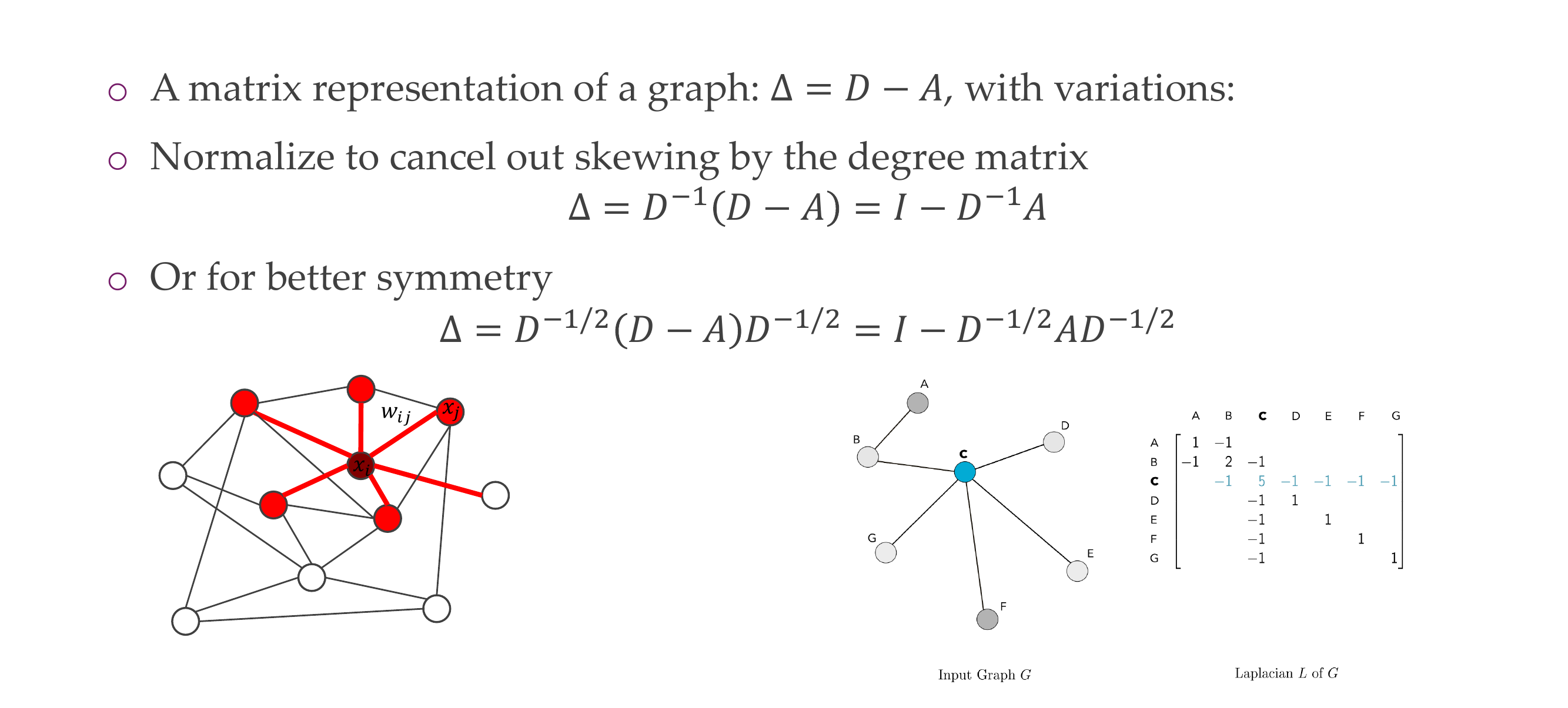
24 Quiz:

Slide 24

25 Graph Laplacian

Slide 25

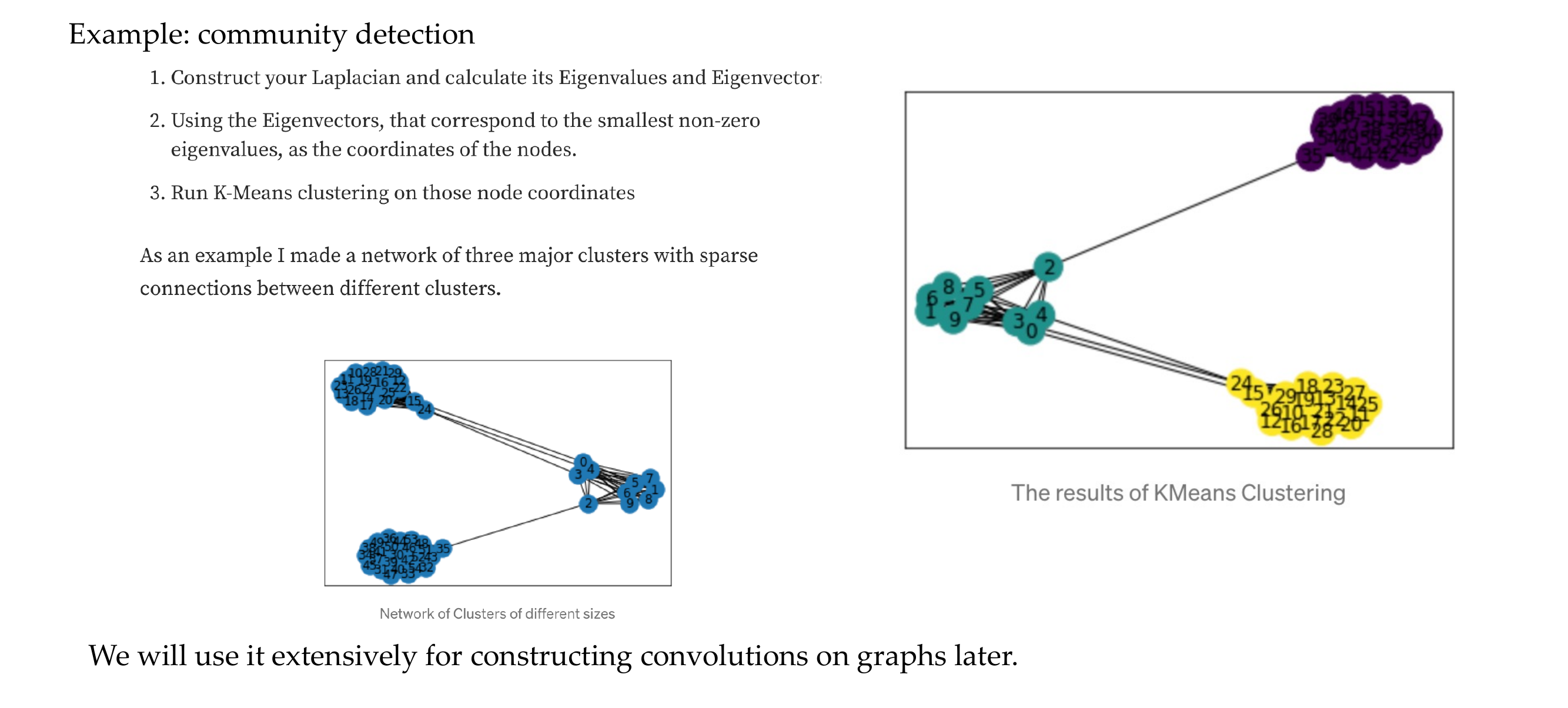
26 Graph Laplacian: meaning

Slide 26

27 Applications of the Graph Laplacian

Slide 27

28 Applied Laplacian written out:

Slide 28

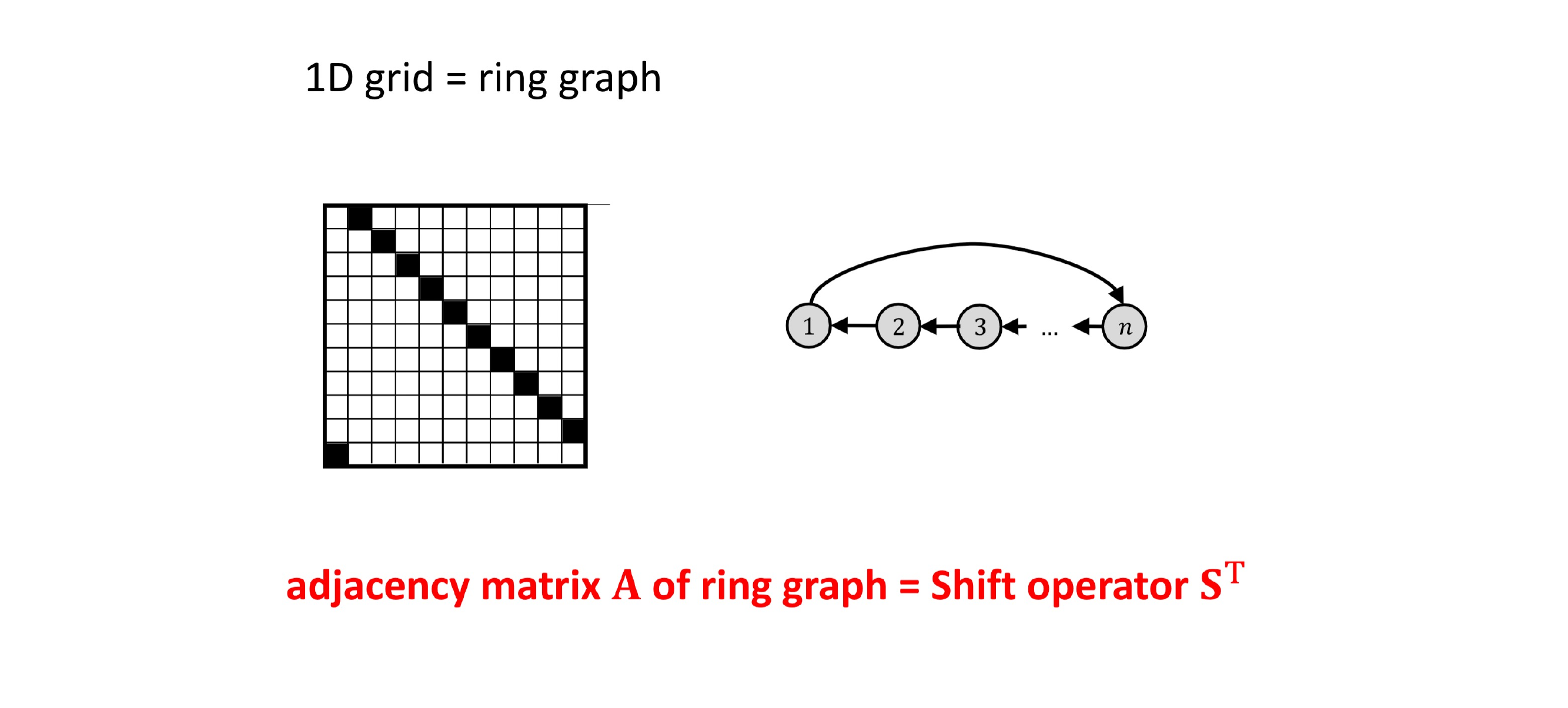
29 Title

Slide 29

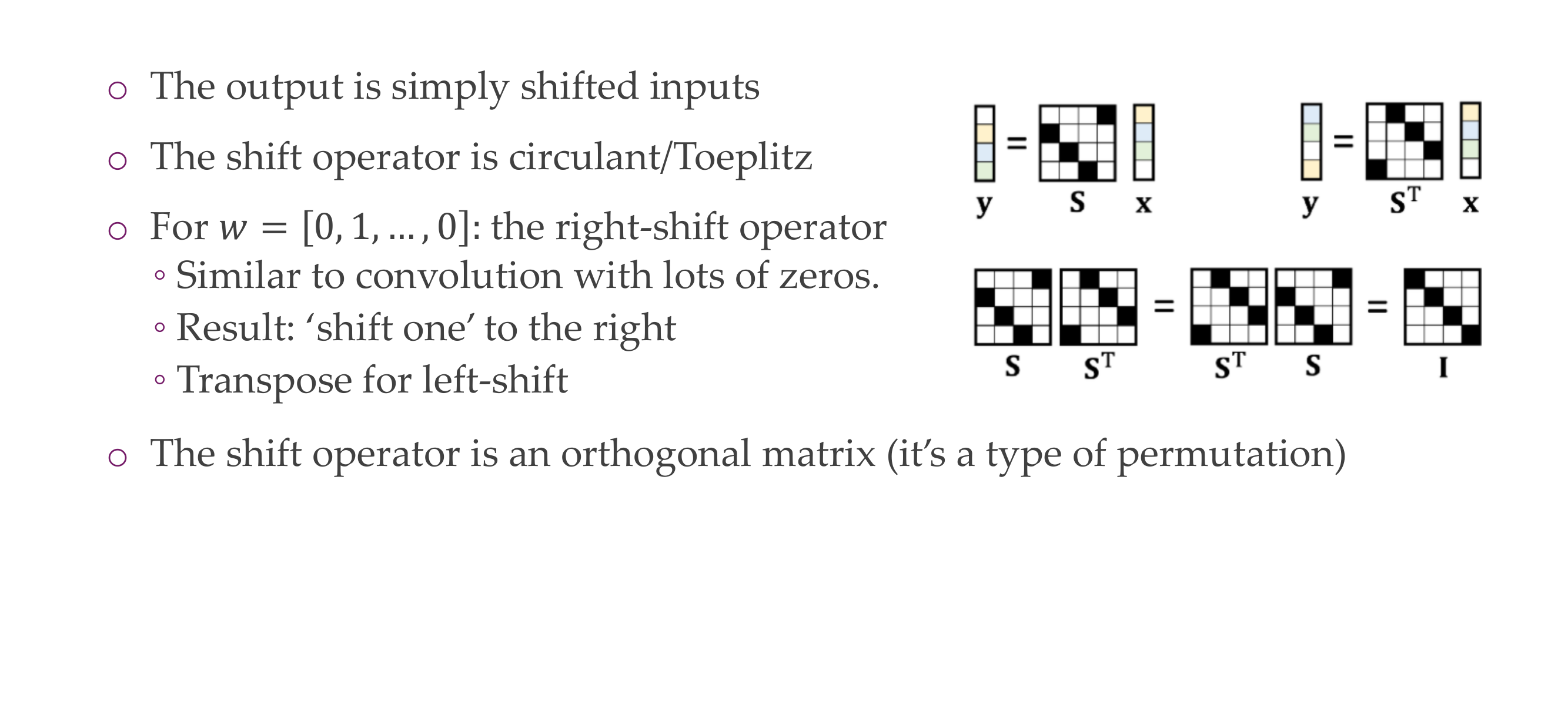
30 The shift operator, a special circulant matrix

Slide 30

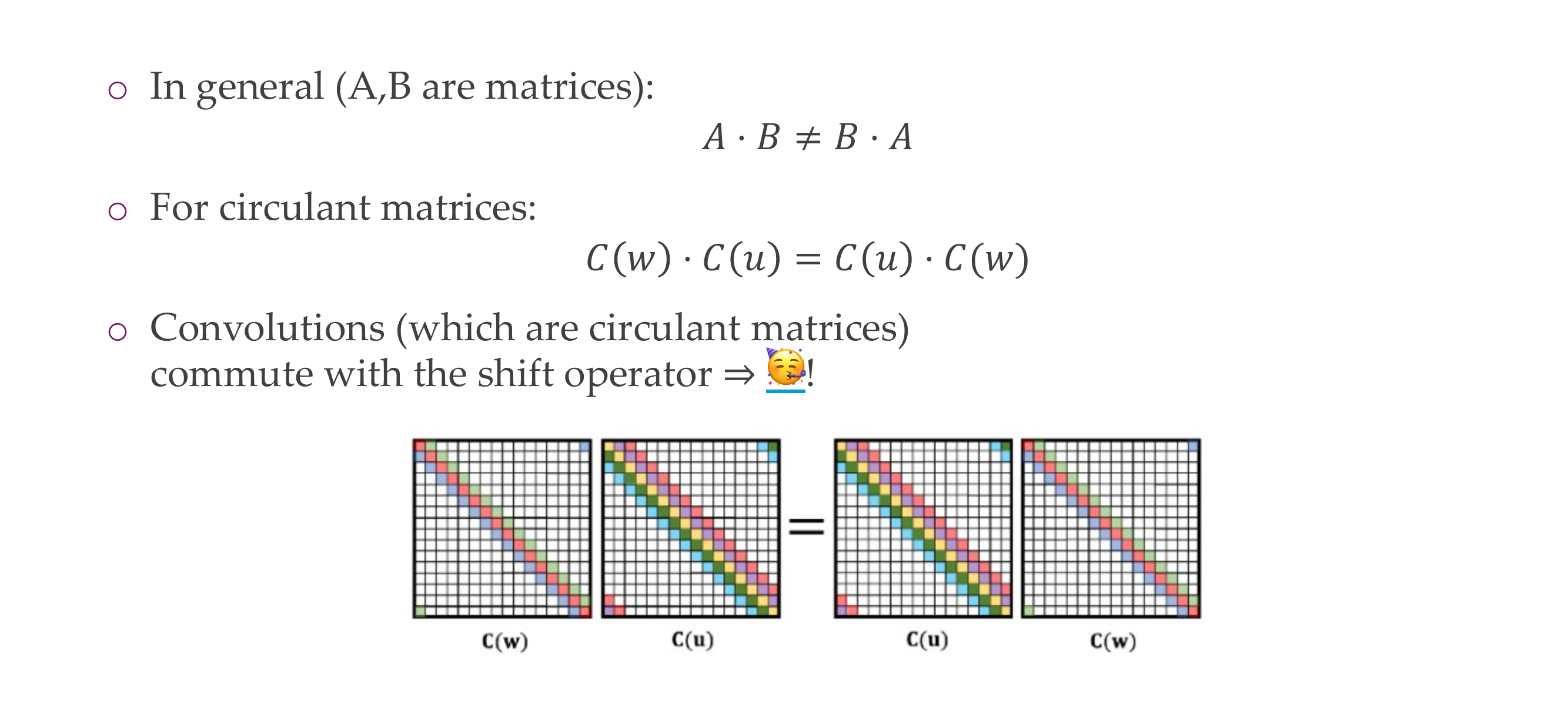
31 Now we want to know:

Slide 31

32 As it turns out: circulant matrices commute

Slide 32

33 What this means: Translation equivariance > circulant matrices/convolutions

Slide 33

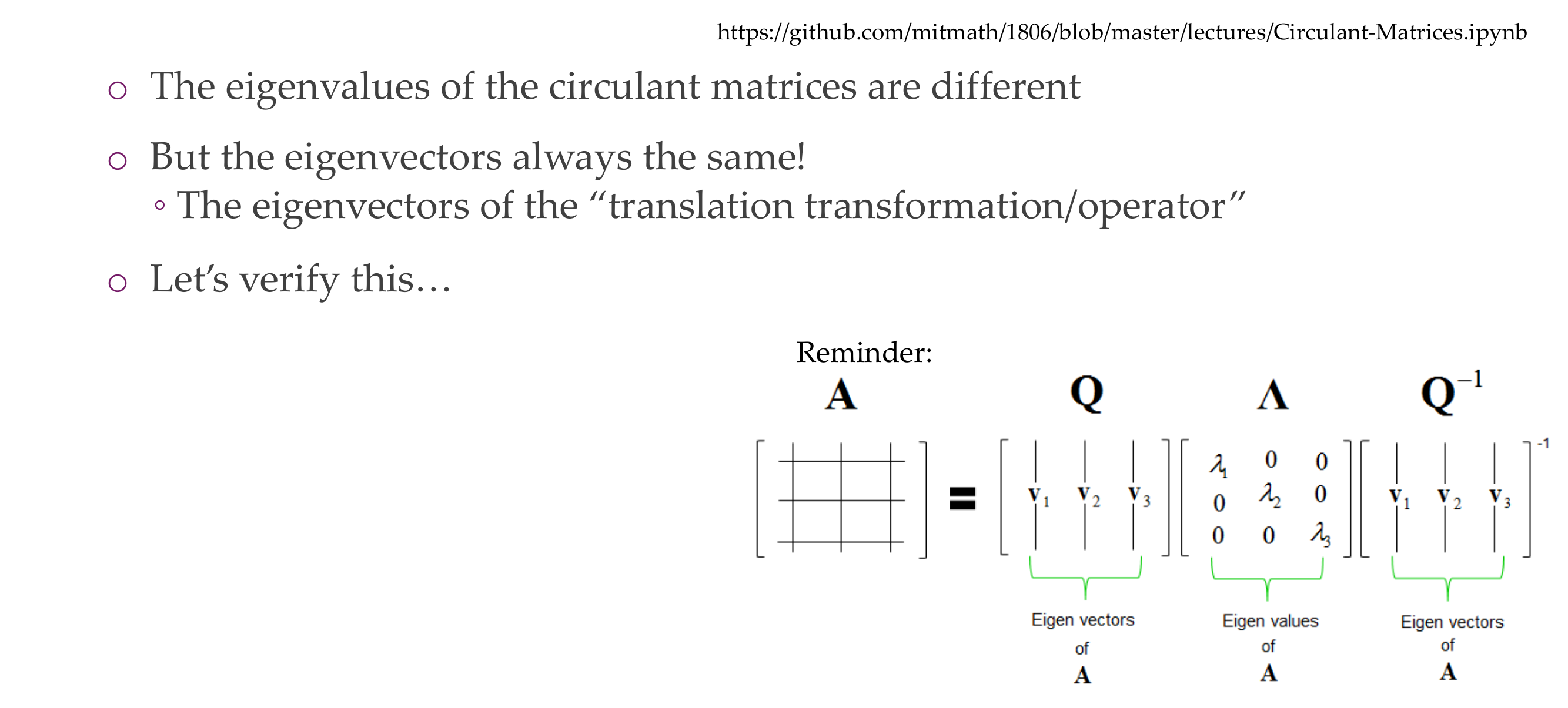
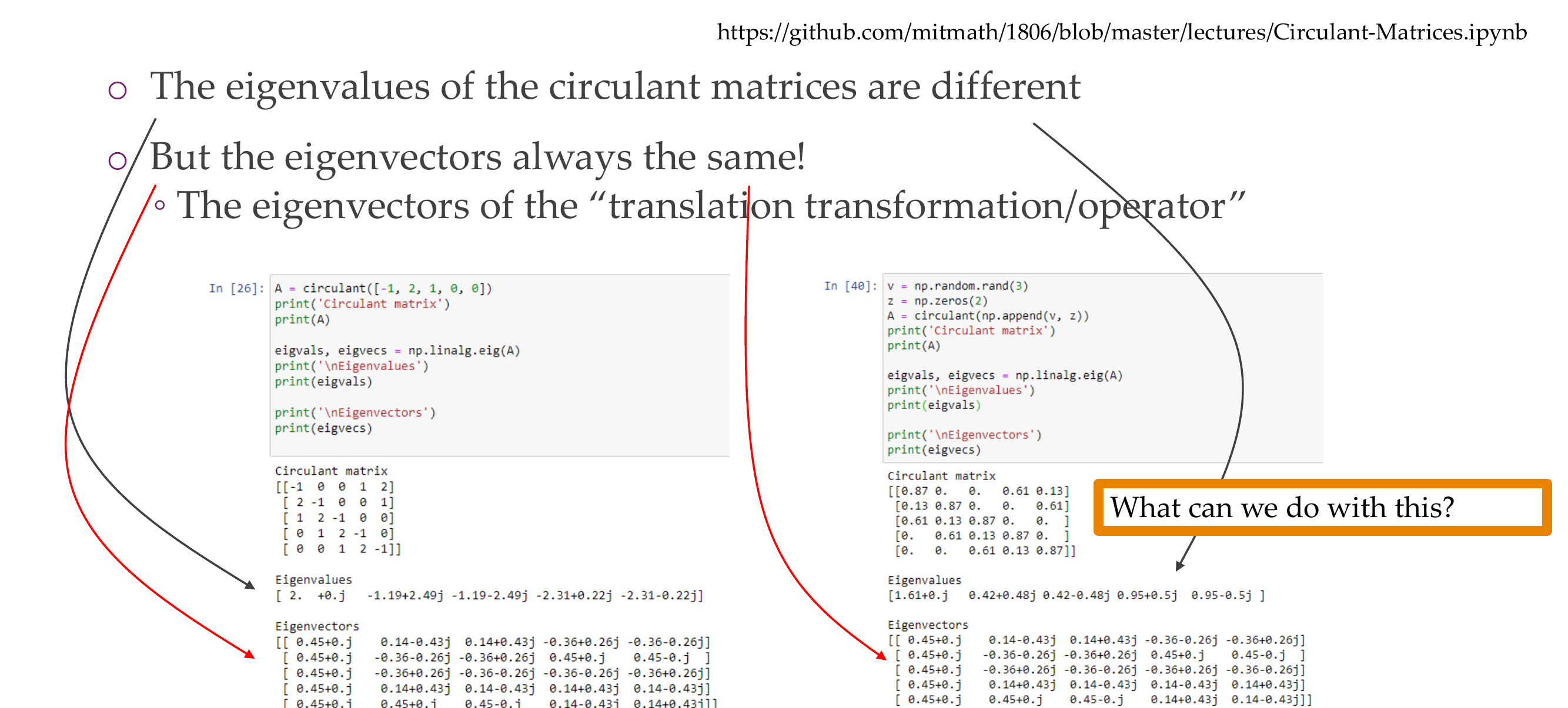
34 Where we are

Slide 34

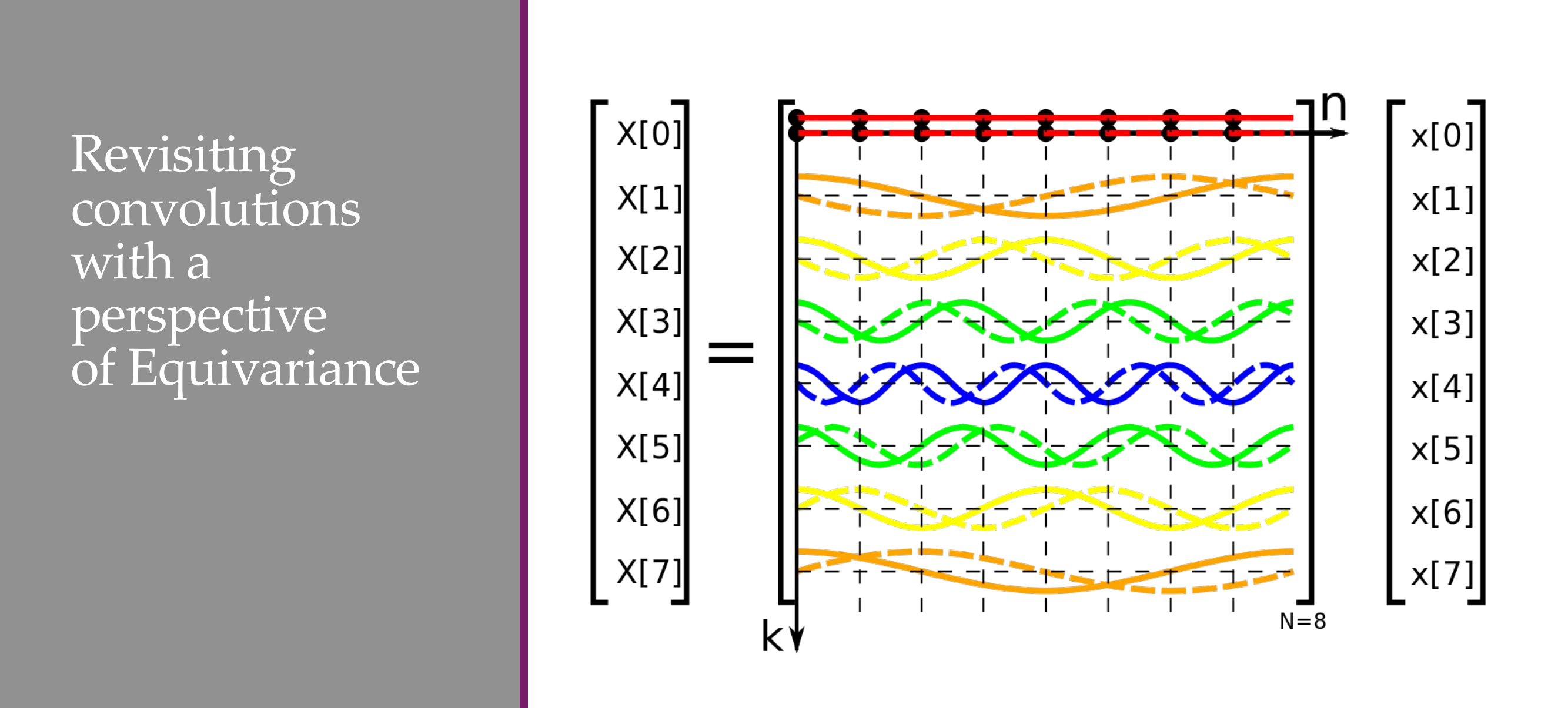
35 Maths: All circulant matrices have the same eigenvectors!

Slide 35

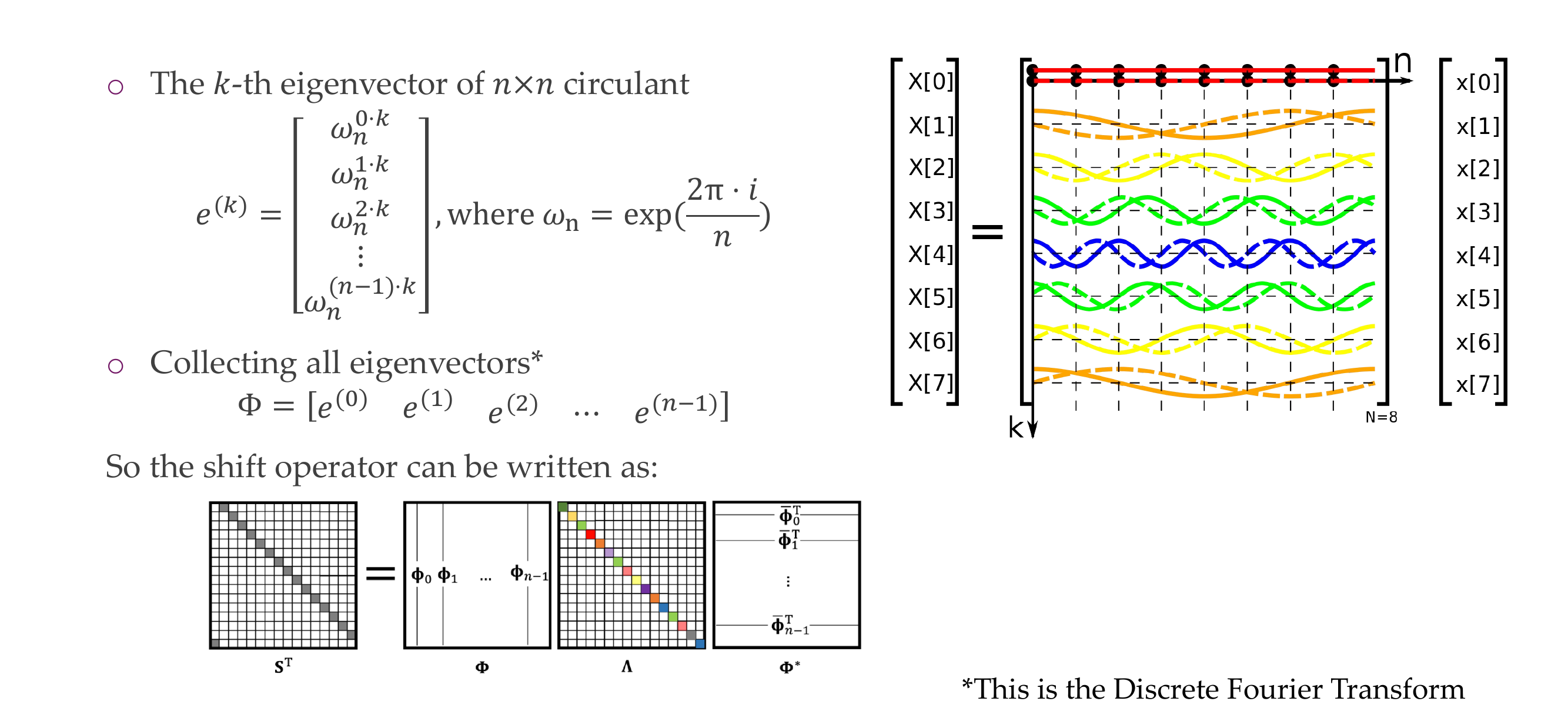
36 All circulant matrices have the same eigenvectors!

Slide 36

37 Circulant eigenvectors © Shift eigenvectors

Slide 37

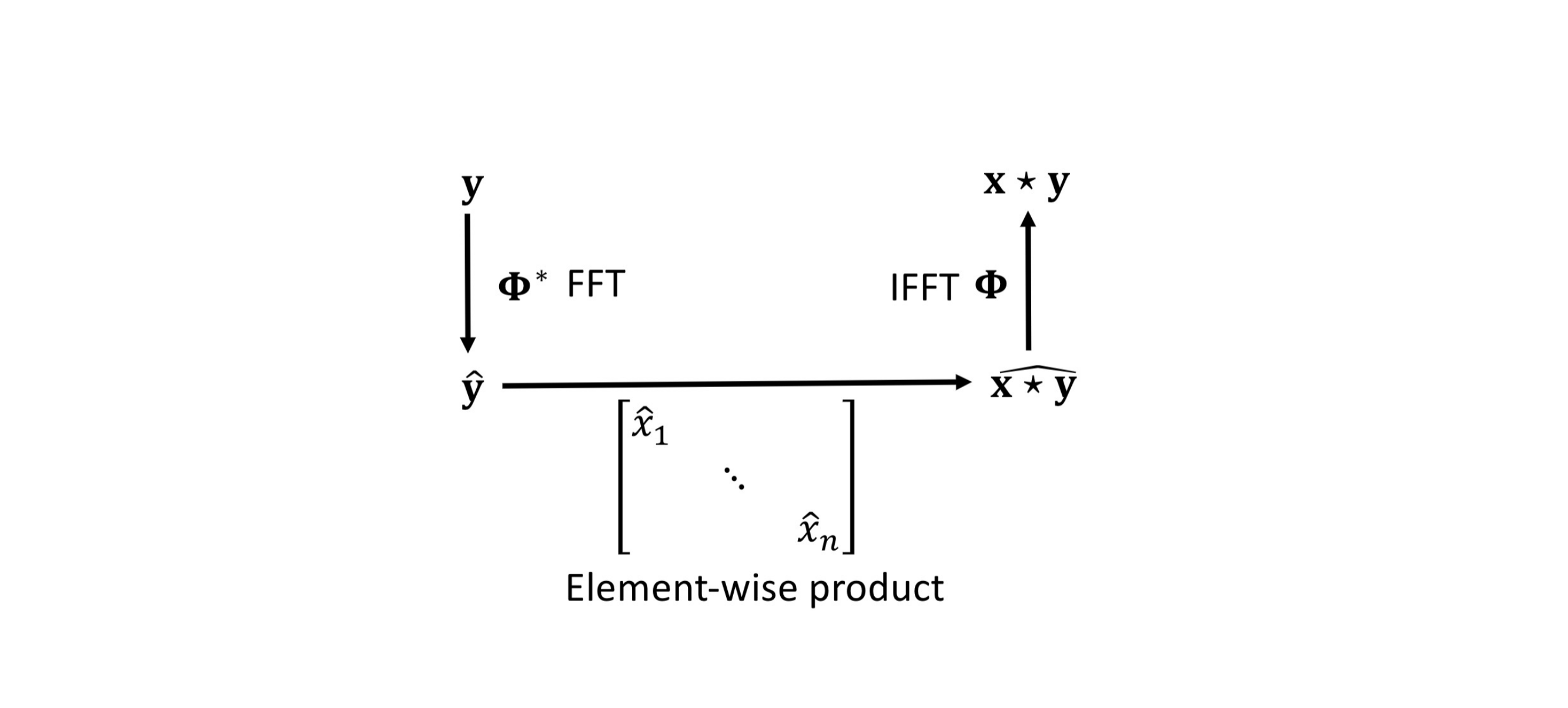
38 But first: What are the eigenvectors of the shift operator

Slide 38

39 Computing a convolution in the frequency domain

Slide 39

40 Convolution Theorem

Slide 40

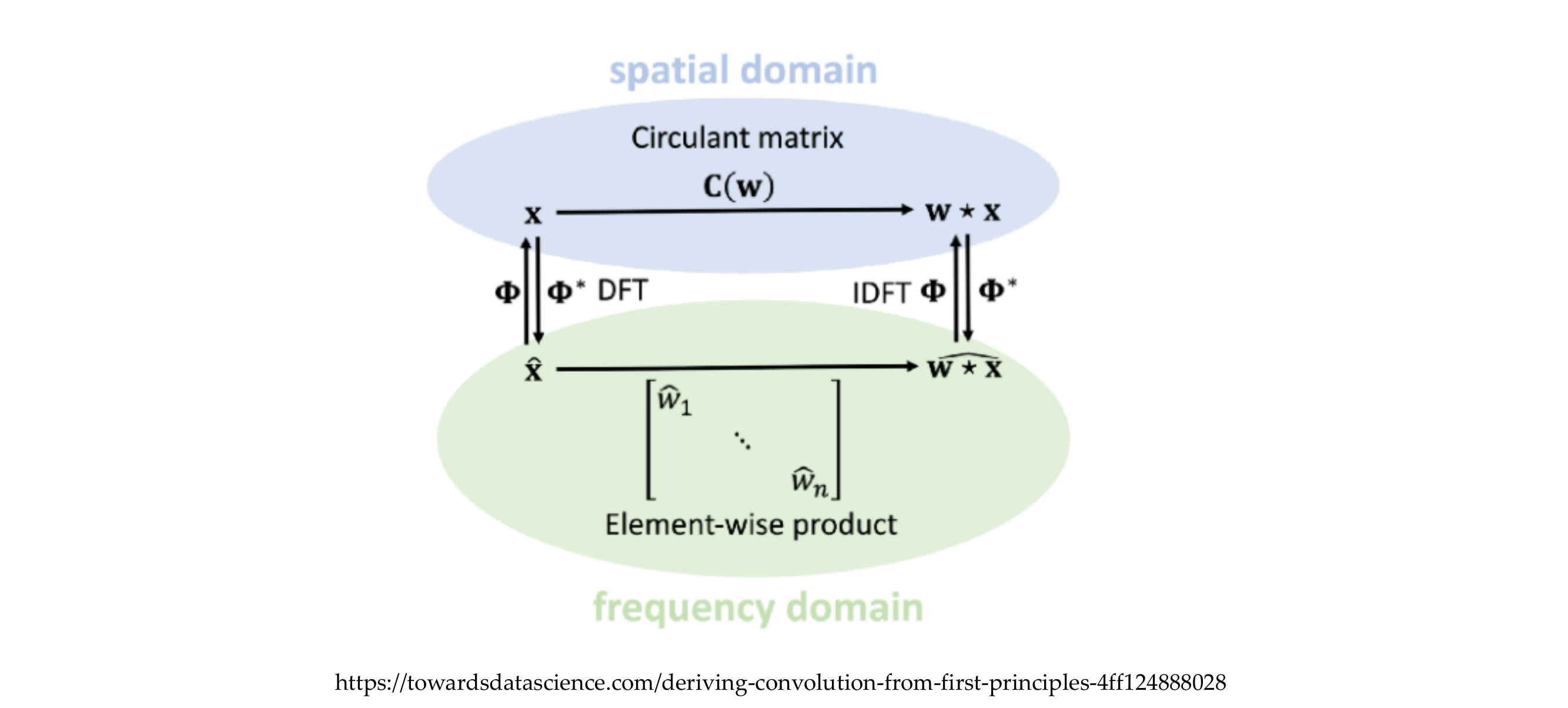
41 Convolution theorem

Slide 41

42 Frequency representation:

Slide 42

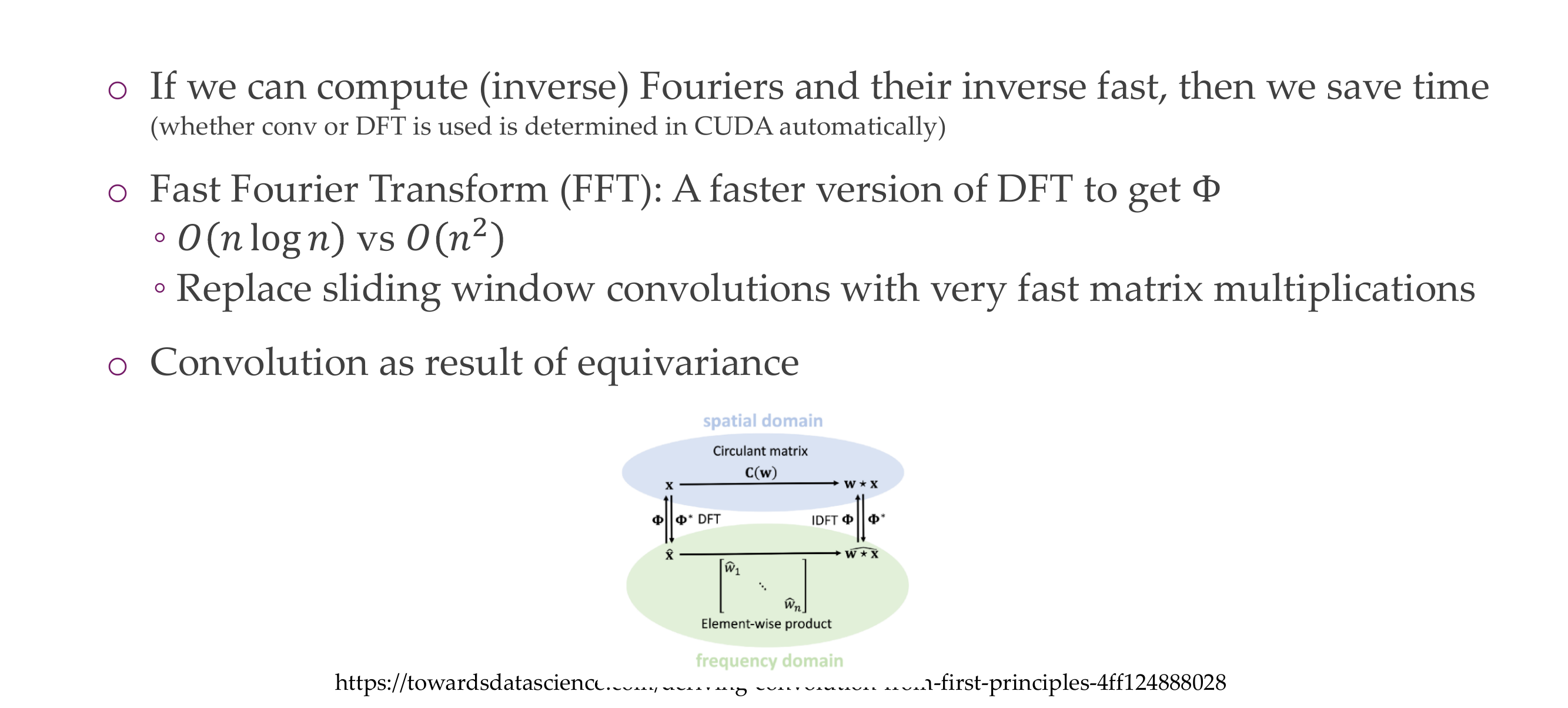
43 ; Quiz: Remember the Fourier transform for images: |

Slide 43

44 Convolution theorem: x * w = ®- (A(w) - (®* - x))

Slide 44

45 Implications

Slide 45

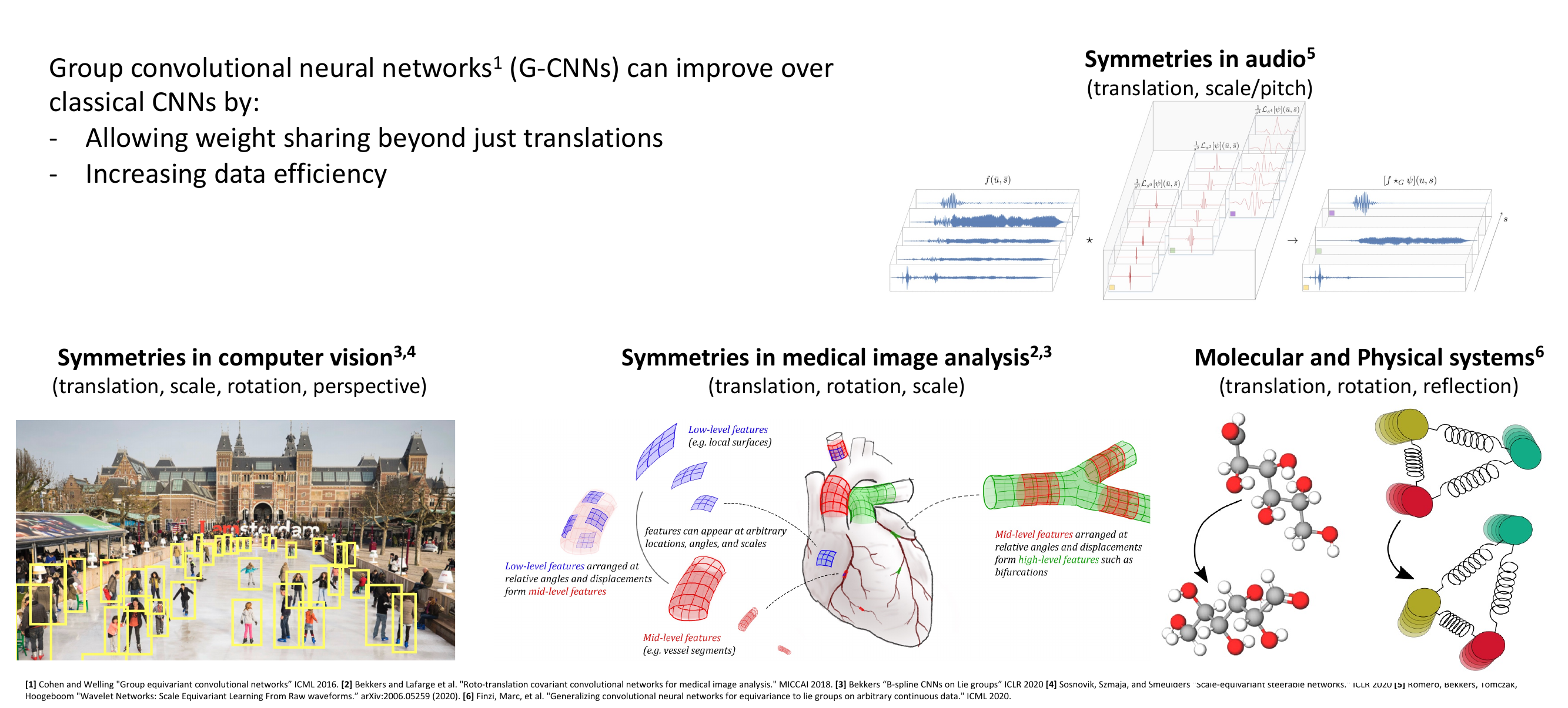
46 If translation equivariance leads to CNNs, what else is there?

Slide 46

47 A large field: Group Equivariant Deep Learning

Slide 47

48 Circulant matrices

Slide 48

49 “I was lucky…

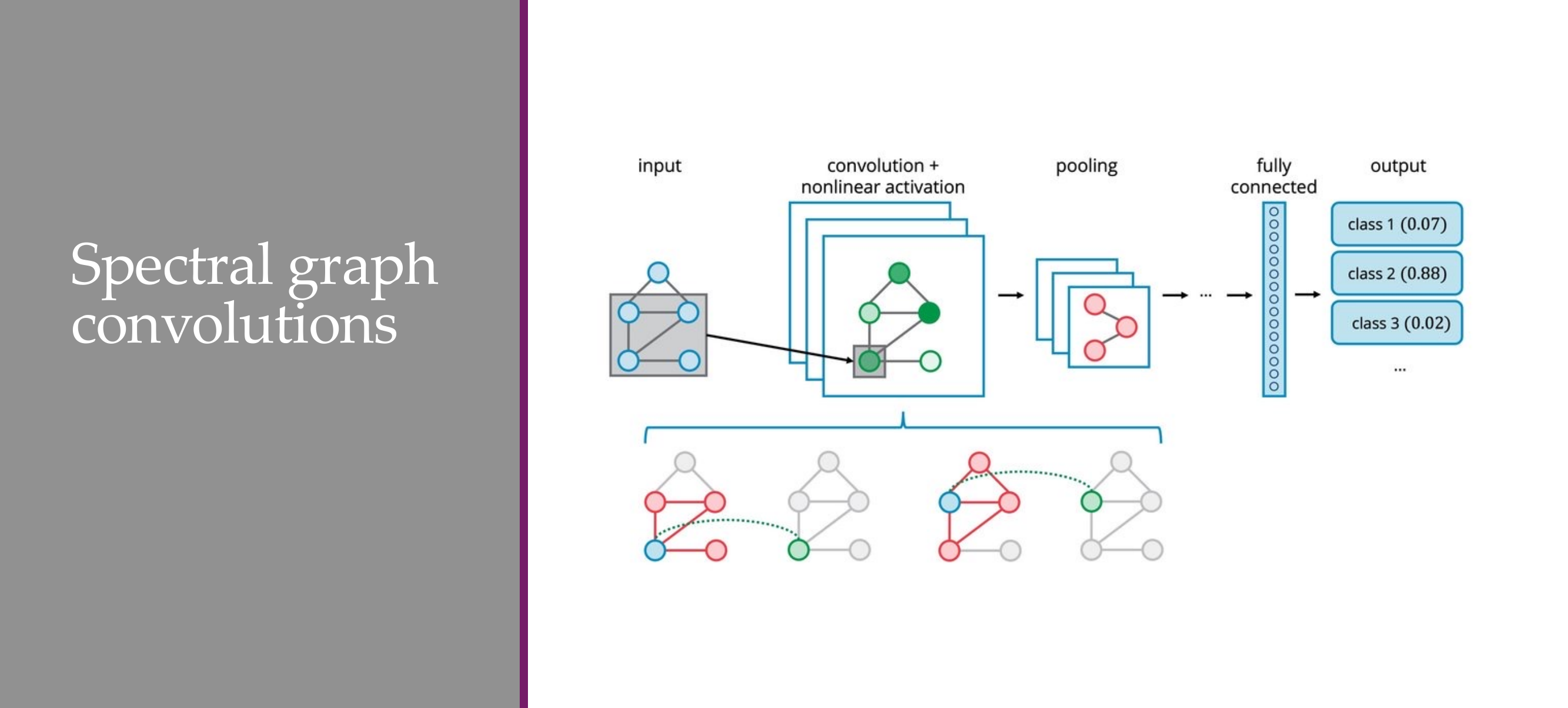
How research gets done part 6

Slide 49

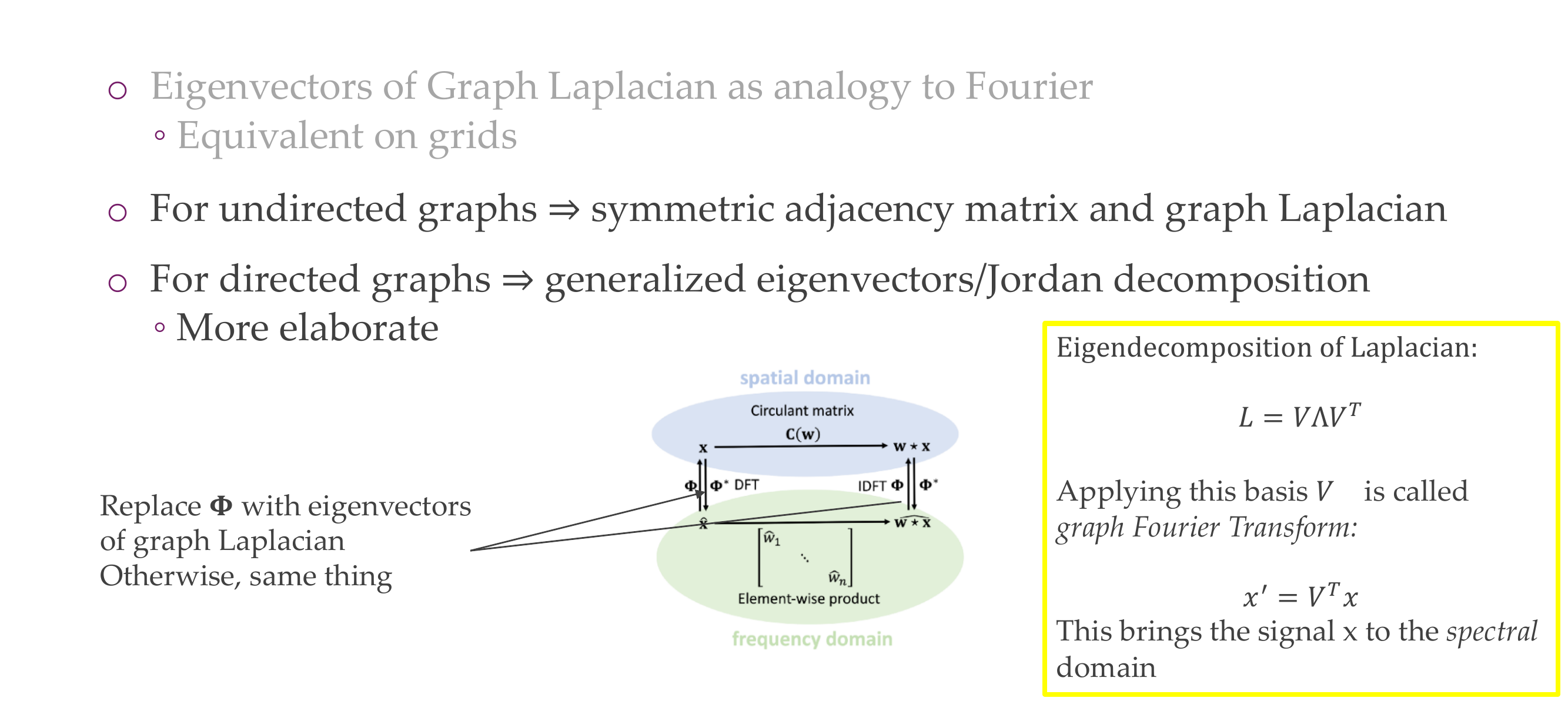
50 Title

Slide 50

51 From convolutions to spectral graph convolutions

Slide 51

52 Approach: Use Eigenvectors of Graph Laplacian to replace Fourier

Slide 52

53 Actually:

Slide 53

54 Further details

Slide 54

55 In analogy to convolutions in frequency domain:

We now define spectral graph convolutions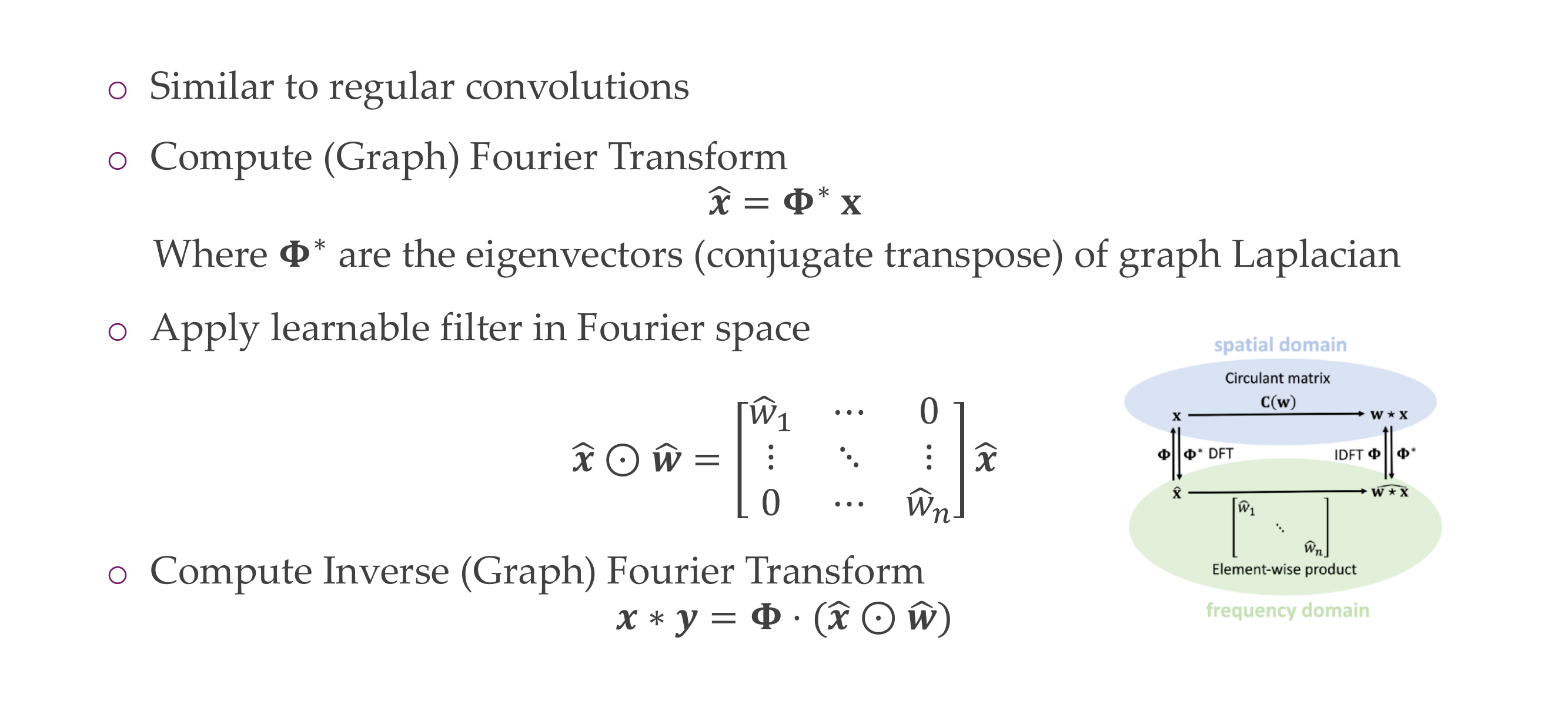

Slide 55

56 Where we are, part 2

Slide 56

57 Why the graph Laplacian*?

Slide 57

58 Spectral graph convolution

Slide 58

59 Some drawbacks of this variant

Slide 59

60 Easy to increase the field of view with powers of the Laplacian

Slide 60

61 Putting it together: stacking graph convolutions

Slide 61

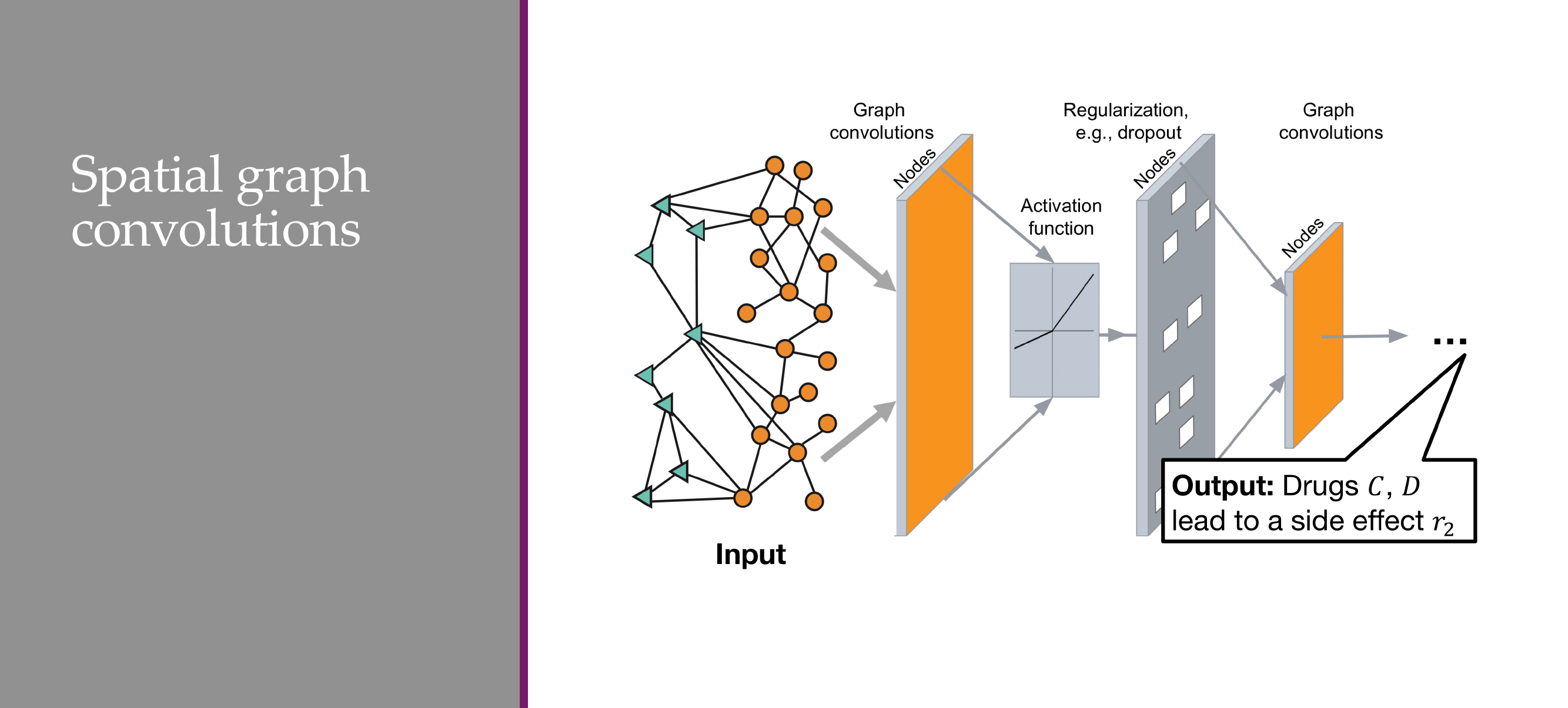
62 . Quiz: What nronerties does this nolvnomial variant have? |

Slide 62

63 Some drawbacks of this variant now

Slide 63

64 Title

Slide 64

65 A FF fF F Fg

Slide 65

66 Graph convolutions

Slide 66

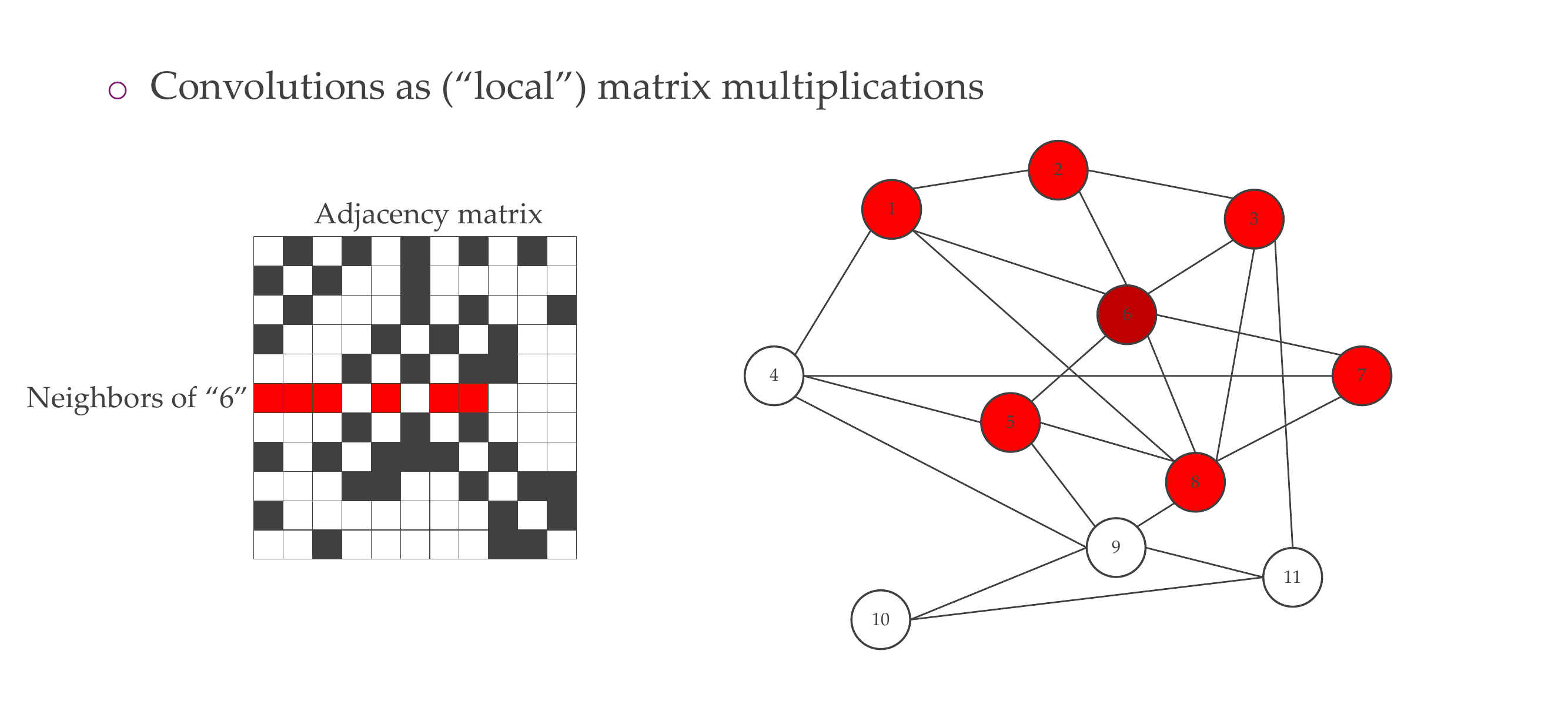
67 What can we use from the spectral approach?

Slide 67

68 Graph Convolutional Networks (GCN)

Slide 68

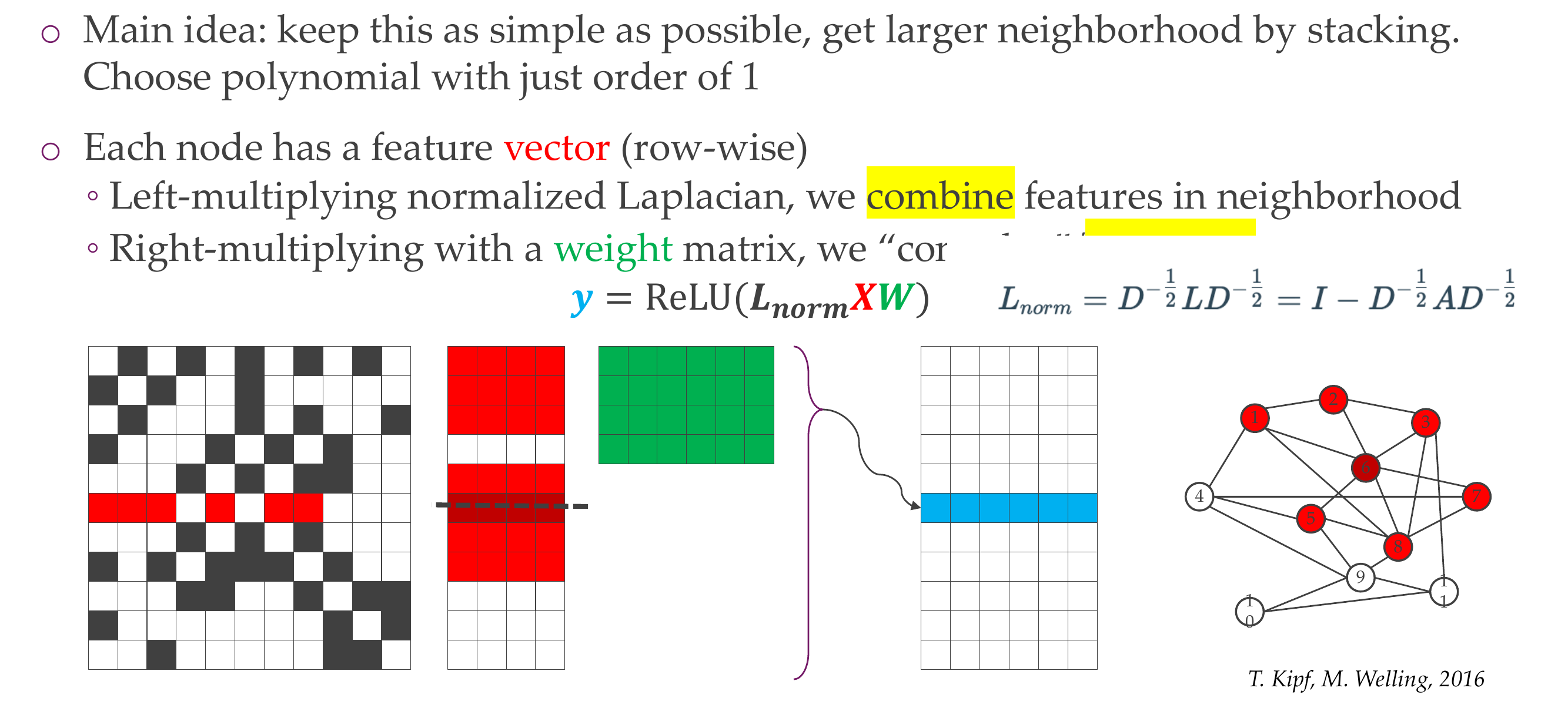
69 Graph Convolutional Networks (GCN)

Slide 69

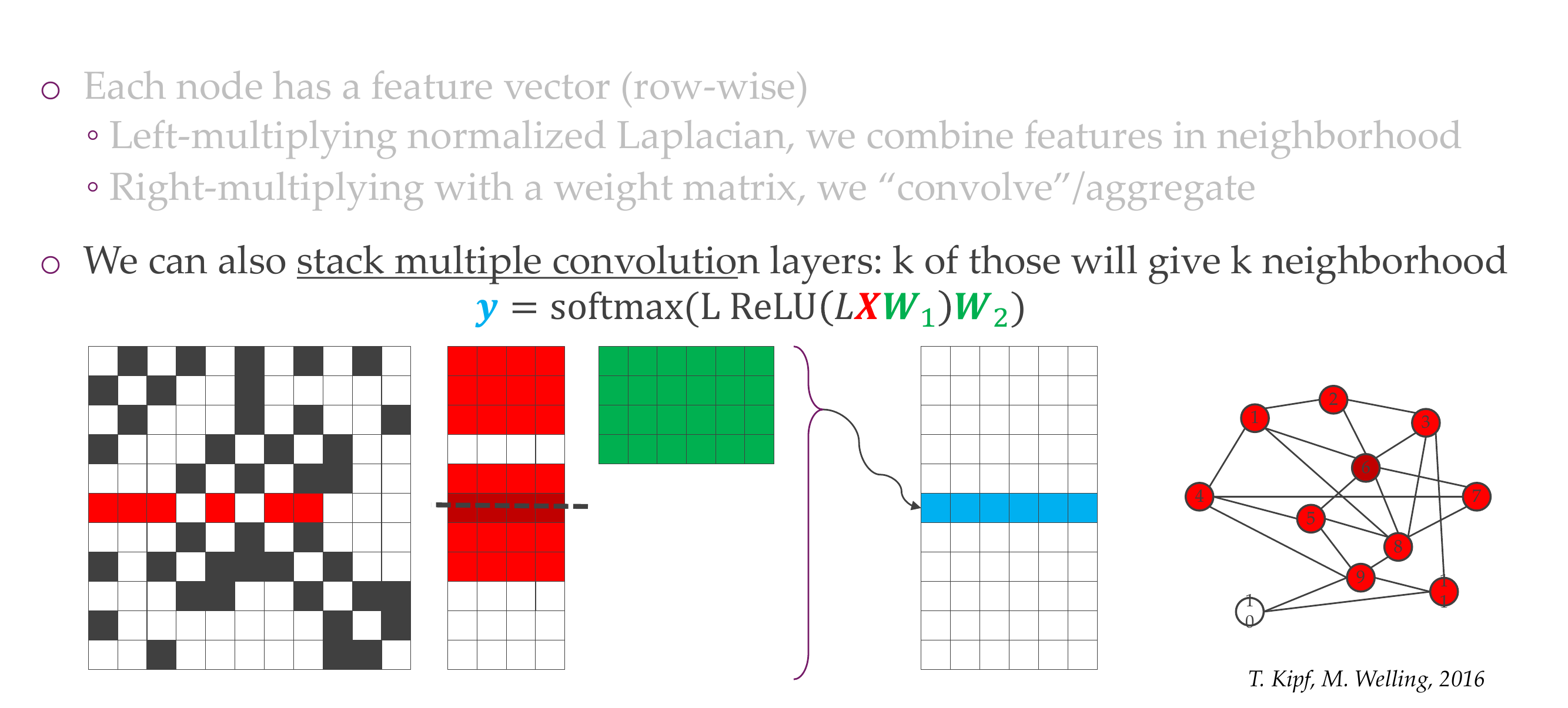
70 Putting it together:

Slide 70

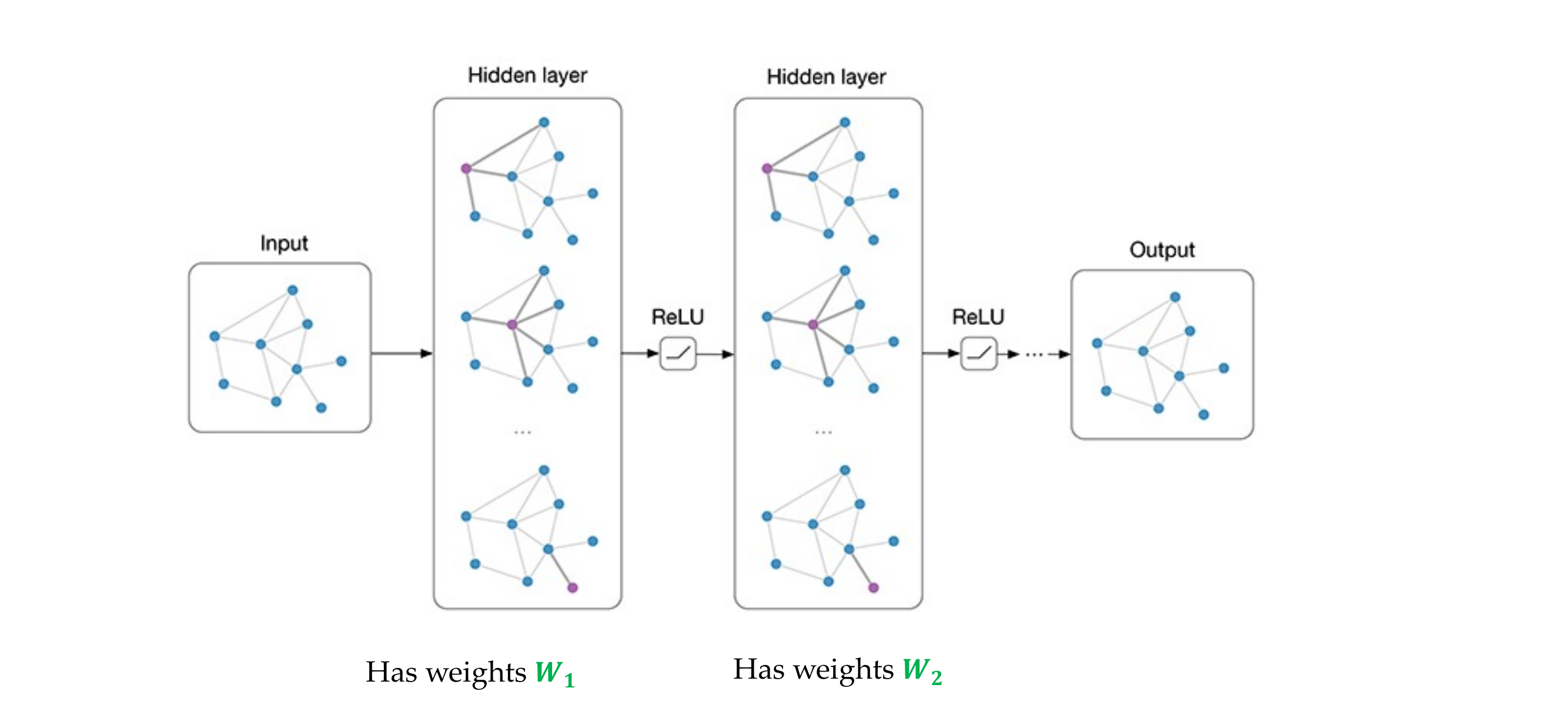
71 Other kind of aggregation: Graph Attention Networks (GAT)

Slide 71

72 Self-attention for graph convolutions

Slide 72

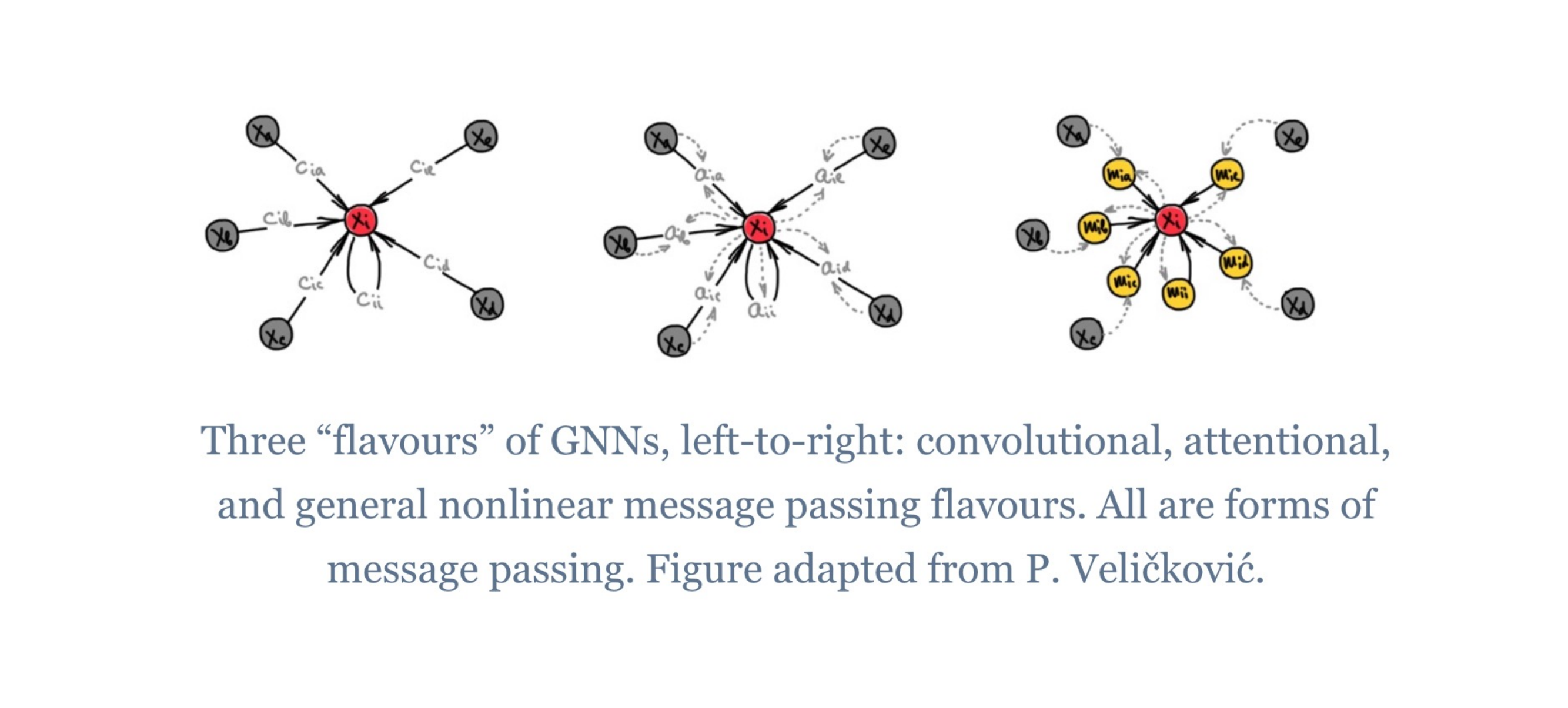
73 Connection to transformers

Slide 73

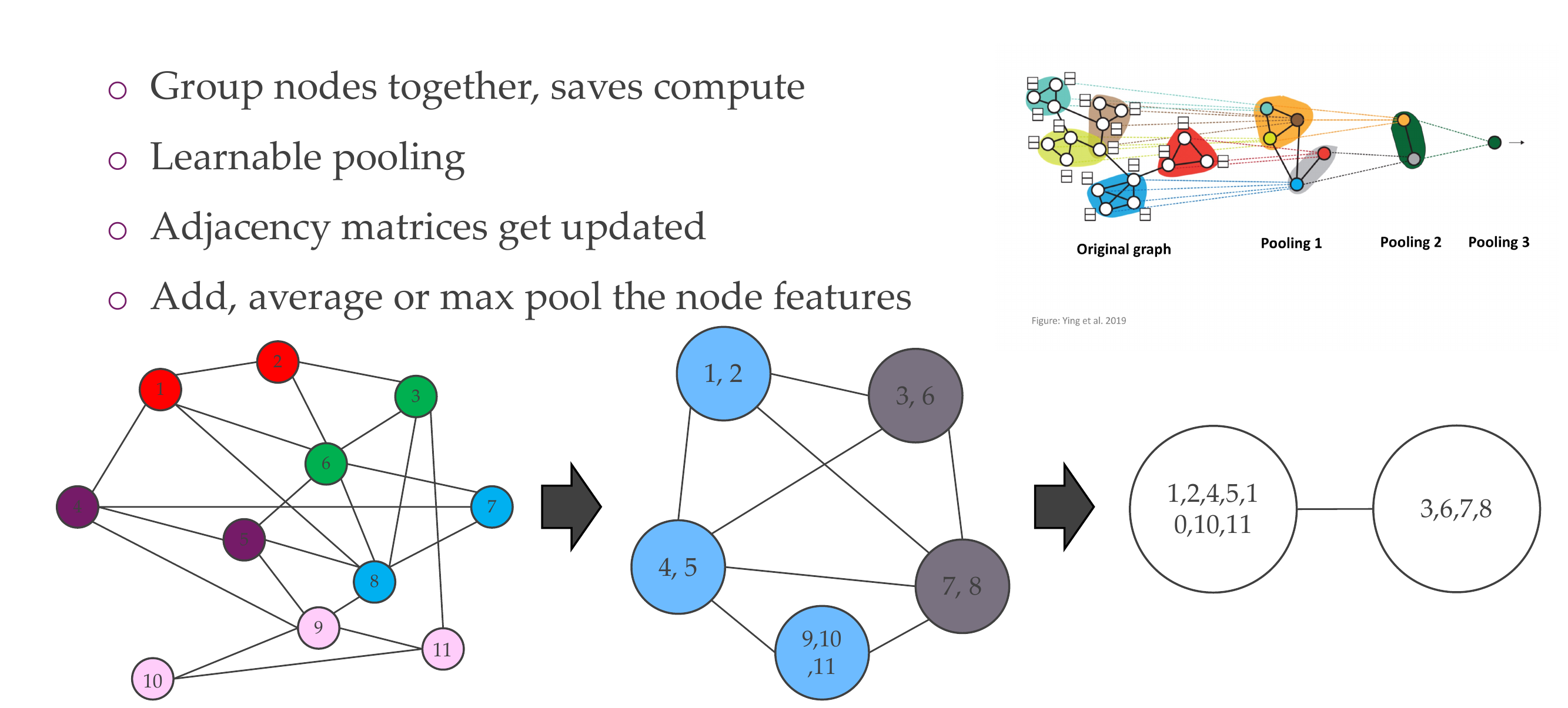
74 Message Passing Neural Network (MPNN)

Slide 74

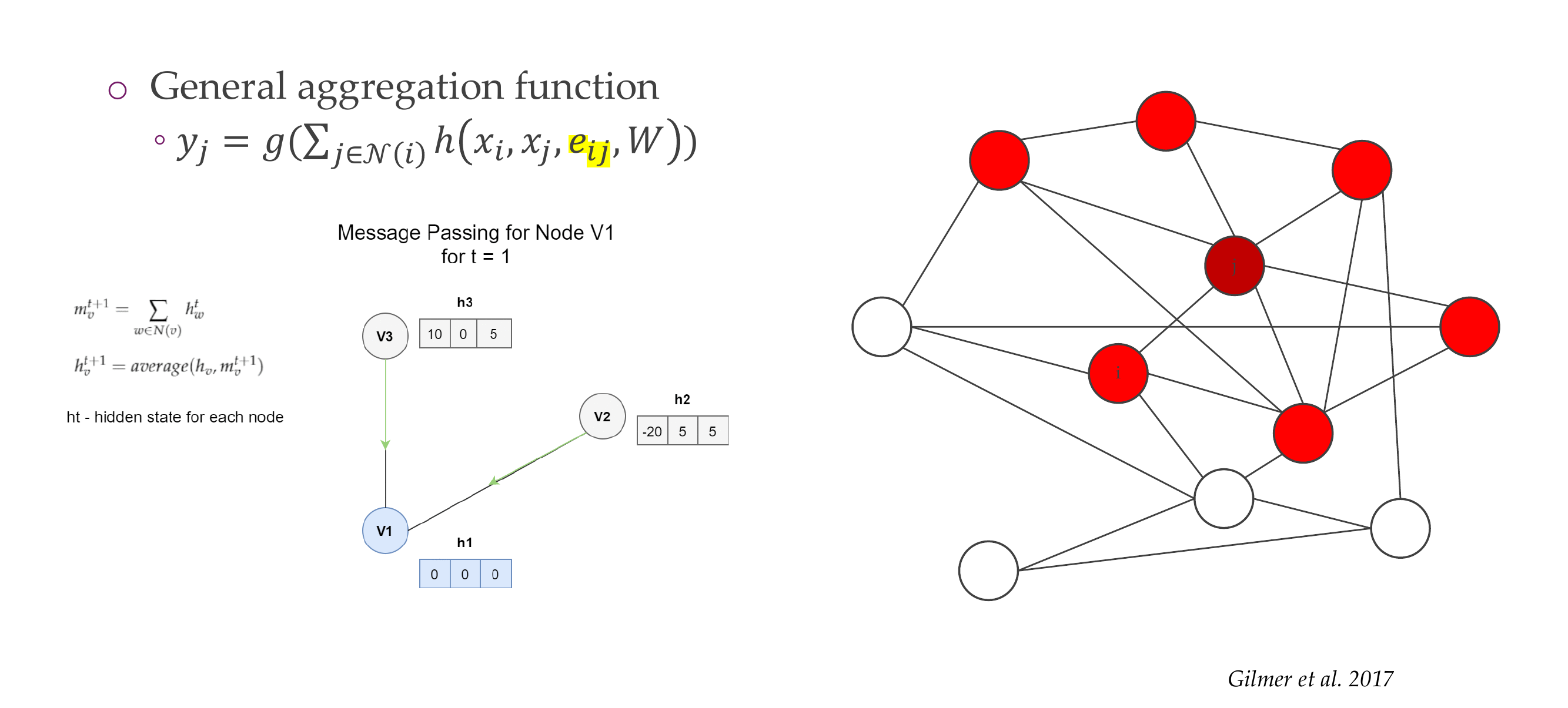
75 PyTorch Geometric baseclass

Slide 75

76 Overview

Slide 76

77 Finally, a note about coarsening graphs

Slide 77

78 Where we are, part 3

Slide 78

79 The last few lectures

Slide 79

80 Title

Slide 80

81 Title

Slide 81